Маргарита Акулич - Статистические методы, используемые в маркетинговых исследованиях

Построение обыкновенной регрессионной модели линейного типа с зависимыми бинарными переменными не допускается ввиду того, что если это построение будет иметь место, предсказанные значения зависимой переменной интерпретировать окажется практически невозможно.

Измерения значений факторов в моделях бинарного выбора – только количественные. В эти модели допускается включение категориальных переменных (выступающих в качестве факторов). В данных моделях обеспечивается построение регрессионной модели зависимости с принятием во внимание вероятности, что результативной дихотомической переменной будет принято значение 0 или 1, если значение факторов – заданное.

Для того чтобы смоделировать вероятность зависимой дихотомической переменной, нужно произвести подбор специальной монотонно возрастающей функции, значения которой могут варьироваться лишь от 0 до 1.

В моделях бинарного выбора в качестве специальной функции может быть выбрана функция: 1) логистическая; 2) стандартного нормального распределения.

Если модель бинарного выбора построена на базе логистической функции, то она рассматривается как логистическая регрессия или логит-модель. Если модель бинарного выбора построена на базе функции, стандартного нормального распределения, то ее рассматривают как пробит-модель.

Посредством логистической регрессии осуществляется прогнозирование вероятности отклика для зависимой переменной от переменных независимых, которые включены в модель. Прогнозные значения вероятности можно использовать для разделения наблюдений на две группы.

При построении модели регрессии логистической можно осуществить отдельный анализ – анализ Receiver Operator Characteristic (ROC-кривых). Посредством данного анализа можно осуществить выбор оптимального порогового значения вероятности для классификации. ROC-кривую используют, чтобы представить результаты бинарной классификации и оценки уровня ее эффективности.

Использование логистической регрессии распространяется на решение задач, связанных с моделированием взаимосвязи и классификацией наблюдений. Она находит применение в скоринге: банковском (на ее основе возможно построение рейтинга заемщиков и управления кредитными рисками); потребительском (для моделирования потребительского поведения).

Регрессия мультиномиальная логистическая

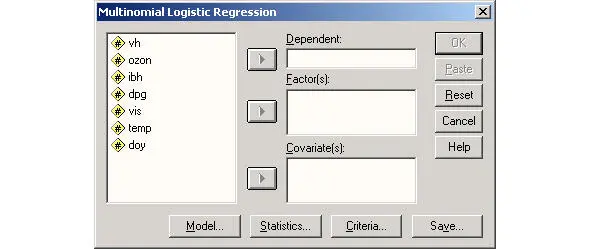
Фото из источника в списке литературы [5]

В качестве логистической регрессии мультиномиальной рассматривают общий случай модели логистической регрессии, в ней у зависимой переменной имеются категории в количестве более двух.

Измерение зависимой переменной (ковариаты) в рассматриваемой регрессии возможно в таких шкалах, как порядковая и номинальная. В качестве нее может выступать переменная потребительского выбора торговой марки. Переменные независимые (факторы) могут быть количественными либо категориальными.

В данной модели для каждой из категорий переменной зависимой предусматривается построение уравнения логистической бинарной регрессии. Причем одной из категорий переменной зависимой отводится роль переменной опорной, и происходит сравнение с ней всех других категорий.

Посредством уравнения мультиномиальной логистической регрессии прогнозируется показатель вероятности принадлежности к каждой категории зависимой переменной согласно значениям переменных независимых.

Пробит-модель регрессии

Фото из источника в списке литературы [6]

Пробит-модель является статистической моделью бинарного выбора, используемой для того, чтобы предсказывать вероятность возникновения какого-то события на базе функции нормального стандартного распределения.

Модель пробит-регрессии, подобно модели логистической регрессии, относят к виду моделей бинарного выбора. По этой причине задачи ее построения и функции такие же, как в логит-модели.

В модели пробит-регрессии выражение расчетного значения зависимой переменной выступает в качестве значения функции нормального стандартного закона распределения. Пробит является значением, для которого исследователи вычисляют функцию нормального стандартного распределения. Имеет место зависимость значения пробита от комбинированных линейных значений факторных переменных. Для пробит-модели (также как и для логит-модели) зависимая переменная – дихотомическая. К факторам в пробит-модели предъявляется требование, чтобы они были количественно выраженными либо категориальными, но преобразованными в переменные дихотомические.