Леонард Млодинов - Кратчайшая история времени

Теория относительности, сформулированная Эйнштейном в 1905 году, называется специальной теорией относительности. Дело в том, что хотя эта теория успешно объясняла постоянство скорости света для всех наблюдателей, а также все происходящее при движении объектов со скоростями, близкими к скорости света, она была несовместима с ньютоновской теорией тяготения. Согласно теории Ньютона в любой момент времени тела притягиваются друг к другу с силой, которая зависит от расстояния между ними именно в этот момент. Следовательно, при перемещении одного из тел сила его воздействия на другое тело должна мгновенно измениться. Если бы, скажем, Солнце внезапно исчезнет, то согласно теории Максвелла тьма накроет Землю лишь через восемь минут (именно столько времени затрачивает свет, чтобы преодолеть расстояние от Солнца до нашей планеты). Но согласно ньютоновской теории тяготения Земля немедленно перестанет чувствовать притяжение Солнца и тут же «слетит» с орбиты. Таким образом, гравитационный эффект от исчезновения Солнца настигнет нас с бесконечной скоростью, а не со скоростью света или меньшей, как этого требует специальная теория относительности. Между 1908 и 1914 годами Эйнштейн предпринял ряд неудачных попыток построить теорию тяготения, совместимую со специальной теорией относительности. Наконец в 1915 году он предложил еще более революционную теорию, которая теперь известна как общая теория относительности.

В основе эйнштейновской общей теории относительности лежит революционная гипотеза, согласно которой тяготение существенно отличается от других сил и является следствием того, что, вопреки привычным представлениям, форма пространства-времени «неплоская». В общей теории относительности пространство-время искривлено или «деформировано» распределенной в нем массой и энергией. Тела, такие как Земля, движутся по криволинейным орбитам не потому, что их принуждает к этому сила тяготения, а потому что такие орбиты представляют собой кратчайший путь в искривленном пространстве. Это так называемые геодезические – ближайший аналог прямого пути в плоском пространстве. Математически геодезическая определяется как кратчайший (или самый длинный) путь между двумя соседними точками.

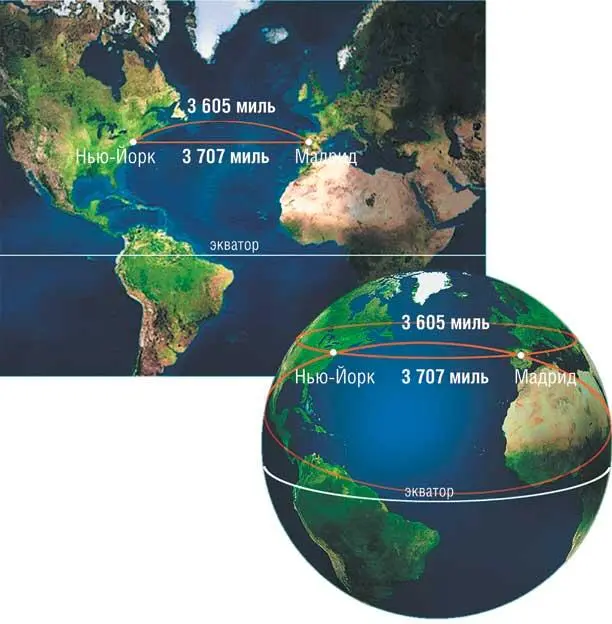
Расстояния на поверхности земного шара. Кратчайший путь между двумя точками на земном шаре проходит вдоль большого круга, который не совпадает с прямой линией на плоской карте

Геометрическая плоскость является примером двумерного плоского пространства, в котором геодезические имеют форму прямых линий. Поверхность Земли – пример двумерного искривленного пространства. Геодезическая на поверхности Земли – это дуга большого круга. Примером большого круга может служить экватор, а также любой круг, центр которого совпадает с центром Земли. Эти круги называются «большими», потому что это самые большие окружности, которые можно «начертить» на поверхности Земли. Поскольку геодезическая – кратчайший путь между двумя аэропортами, то именно такой маршрут предлагает пилоту навигатор. Например, из Нью-Йорка в Мадрид можно лететь по компасу почти точно на восток вдоль меридиана (оба города находятся примерно на одной широте) и путь протянется на 3707 миль [5966 км], но если лететь по большому кругу, сначала в северо-восточном направлении, постепенно поворачивая на восток и на юго-восток, то путь составит всего 3605 миль [5802 км]. Пусть вас не вводит в заблуждение вид этих двух путей на плоской карте – поверхность Земли на ней неизбежно искажена («уплощена»). Двигаясь «прямо» на восток, вы на самом летите не по прямой, по крайней мере, не по прямой в смысле кратчайшего пути или геодезической линии.

Путь тени космического корабля. В проекции на двумерную поверхность земного шара тень движущегося прямолинейно космического корабля выглядит искривленной

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.