Леонид Хренов - Время и календарь

Поскольку все существующие календарные формулы опубликованы без их вывода, можно считать, что они были получены методом подбора. Этим и объясняется большая их разновидность. При этом многие формулы действительны только для нового стиля и не позволяют непосредственно определять день недели календарных событий, имевших место в нашей стране до 1918 г. Формулы отличаются еще и тем, что в одних за первый день недели принято воскресенье, а в других — понедельник. (Только с 1976 г. согласно стандарту Международной организации стандартов 2015–1976 за первый день недели принят понедельник.)

Большинство формул из-за своей сложности трудно запоминаются. Для некоторых требуется подсчитывать количество дней, прошедших от начала года до заданной даты, а для других — для каждого месяца определять свой коэффициент.

При выводе формулы примем следующие обозначения: К — календарное число месяца; М — коэффициент месяца; J — полный номер года н. э.; Д — порядковый номер года в столетии; Г' — сдвиг дней недели по годам; Г — коэффициент года; В — коэффициент века; С — число полных прошедших столетий; [] — целая часть частного от деления (неполное частное); | | — остаток от деления, причем если делимое меньше делителя, остаток равен делимому; d — порядковый номер дня недели (0 — воскресенье, вс; 1 — понедельник, пн; 2 — вторник, вт; 3 — среда, ср; 4 — четверг, чт; 5 — пятница, пт; 6 — суббота, сб).

День недели календарной даты определяется как остаток от деления суммы чисел К, М, Г и В на 7:

d = |( K+ M + Г + В) / 7 | (1)

Сделаем предположение, что 1 января 1 г. п. э. был понедельник (= 1). Тогда для дат января первого года день недели будет определяться по формуле

d = |К / 7 |.

Так как в январе 31 день, то день недели в феврале первого года определится по формуле

d = |(К + (31–28)) / 7 | = |(K + 3) / 7 |.

Здесь 28 — ближайшее к 31 число, кратное семи, которое мы вычитаем для упрощения вычислений.

Так как в феврале первого года 28 дней, то день недели в марте определяется так же, как и в феврале. В марте 31 день, поэтому для апреля получим формулу

d = |(К + 3 + (31–28)) / 7 | = |(K + 6) / 7 |.

Аналогично получим формулы для остальных месяцев. В этих формулах числа, прибавляемые к календарному числу К, суть коэффициенты месяцев М, которые мы свели в табл. 9.

Таким образом, день недели для первого года н. э. будет определяться по формуле

d = |(K + M) / 7 |. (2)

Объединив повторяющиеся в табл. 9 значения М для разных месяцев, получим табл. 10.

Так как в простом году 52 недели и один день (365 = 52×7 + 1), то для второго года н. э. календарная формула примет вид

d = |(K + M + 1) / 7 |.

а для третьего

d = |(К + М + 2) / 7 |.

Следующий год (четвертый) — високосный; в нем 366 дней (за счет увеличения числа дней в феврале: 29 вместо 28). Поэтому для 4 г. н. э. календарная формула принимает вид для января и февраля

d = |(K = M + 3) / 7 |.

а для месяцев с марта по декабрь

d = |(K = M + 4) / 7 |.

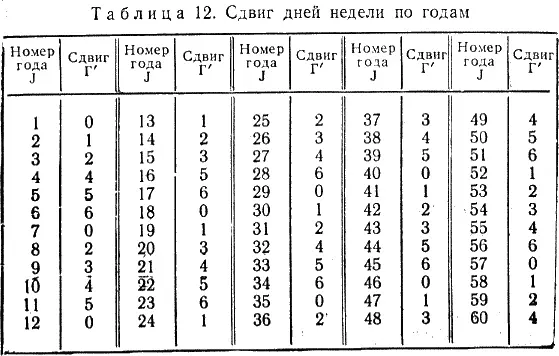
В табл. 11 приведены коэффициенты М для високосных (вис.) и невисокосных — простых (пр.) лет. Так как сдвиг дней недели по годам Г' в четырехлетиях 1–4, 5–8, 9–12 и т. д. происходит одинаково, составим таблиц значений Г' для J от 1 до 60 лет (табл. 12). Мы видим, что в каждом следующем четырехлетии значение сдвига Г' «увеличивается» на 5. Это позволяет выразить его для високосных годов (J вис) в виде формулы

Г' = |(5(Jвис:4) — 1) / 7)|

а для простых (J np ) в виде формулы

Г' = |(5 (J вис: 4) — 1 + (J пр— J вис)) / 7 |,

где J вс— ближайший меньший високосный год [53] Для 1, 2, 3 годов н. э. таким ближайшим високосным годом является «нулевой» год. , а так как

J вис: 4 = [J пр: 4],

(3)

то общей формулой для Г' для простых и високосных годов будет

Г' =|(J + [J: 4] — 1) / 7 |. (3)

Упростим формулу (3), убрав в ней «—1». Чтобы сумма М + Г в формуле (1) осталась неизменной, уменьшим на единицу значения коэффициентов М в табл. 11 (при этом 0 считается равным 7). Новые значения коэффициентов М приведены в табл. 13, а формула (3) примет вид