Рудольф Киппенхан: Рудольф Киппенхан 100 миллиардов солнц: Рождение, жизнь и смерть звезд

Другой важный метод определения расстояний я могу описать лишь приблизительно. Он основан на том, что звезды, принадлежащие к одному скоплению, движутся все в одном направлении с одинаковыми скоростями по параллельным траекториям. Хотя их движение наблюдается как крошечное, неизмеримо малое смещение на небе, для многих скоплений удается заметить, что их параллельные траектории сходятся в одной точке, подобно тому как сходятся рельсы железной дороги в одной точке на горизонте. Эта точка говорит нам о том, в каком направлении движется та или иная группа звезд. Измерив лучевую скорость движения звезд с помощью эффекта Доплера, а также скорость, с которой эти звезды год от года смещаются относительно очень удаленных (неподвижных) звезд, можно определить расстояние до интересующего нас скопления. Задача снова сводится к решению треугольников, но здесь мы не будем вдаваться в подробности. Так было измерено расстояние до многих звездных скоплений, что позволило определить светимость звезд и их положение на диаграмме Г-Р, как рассказывалось в гл. 2.

Можно поступить и наоборот. Если звезды находятся так далеко, что ни один из описанных методов не дает результатов, то пользуются тем фактом, что менее массивные звезды лежат на главной последовательности, и, как положено, светимость каждой соответствует ее цвету. И если я смогу определить цвет звезды главной последовательности какого-либо скопления, то тут же буду знать и ее светимость. Сравнивая светимость звезды с ее блеском (яркостью, которую имеет звезда на небе), я после несложных вычислений определю расстояние до нее, а следовательно, и до звездного скопления.

То, что удалось проникнуть в космос на еще большие расстояния, почти фантастично. По причинам, которые долгое время оставались непонятными, пульсирующие звезды-цефеиды, о которых говорилось в гл. 6, обладают замечательным свойством. Между их периодом и светимостью существует однозначная связь (рис. Б.2). Период изменения блеска цефеид легко установить с помощью регулярных наблюдений, и тогда нетрудно, зная показанную на рис. Б.2 закономерность, определить их светимость, среднюю за период. А сравнивая светимость с блеском звезды, легко вычислить расстояние до нее. Цефеиды обладают очень высокой светимостью, поэтому их можно наблюдать не только в самых отдаленных уголках нашего Млечного Пути, но и среди звезд других галактик. Благодаря этому удалось определить расстояние от нашей собственной Галактики, до галактик, лежащих дальше от нас, чем Туманность Андромеды.

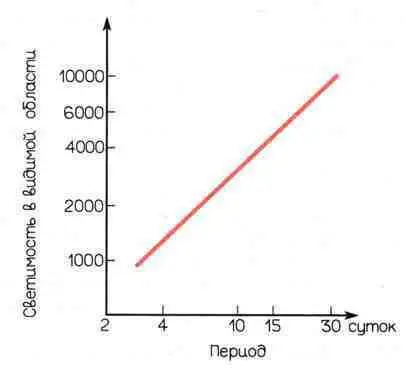
Рис. Б.2. Диаграмма период — светимость переменных звезд типа цефеид. У этих звезд определенному значению периода соответствует вполне определенная светимость. Поскольку период определить легко, нетрудно, зная период, вычислить и светимость звезды, усредненную за период. Зная светимость звезды и ее видимую величину (блеск), можно определить расстояние до звезды.

Несмотря на то что современная техника подарила астрономам точнейшие измерительные устройства и позволила им применять в своих расчетах компьютеры, при определении звездных масс астрономы не продвинулись далеко от методов, восходящих еще к Иоганну Кеплеру и Исааку Ньютону, методов, которым уже триста лет. Начнем с массы Солнца. В поле силы тяжести Солнца Земля движется почти по круговой орбите. При этом она испытывает действие центробежной силы, стремящейся отбросить ее в пространство. Центробежная сила действует против притяжения Земли Солнцем — силы, которая стремится обрушить нашу планету в центр огненного солнечного шара. Земля движется точно по такой траектории, на которой эти противодействующие силы находятся в равновесии. Условие равновесия этих сил дает возможность определить силу, с которой Земля притягивается Солнцем, а, следовательно, и массу последнего по формуле

(радиус орбиты планеты) 3= (гравитационная постоянная) х (масса планеты + масса Солнца) х (период обращения планеты) 2.

Значение гравитационной постоянной известно из физики. Радиус орбиты Земли определяется методом, описанным в приложении Б. Период обращения Земли вокруг Солнца равен одному году. Таким образом, наше уравнение содержит только одно неизвестное, сумму масс Земли и Солнца, и его нетрудно решить. Так как масса Земли ничтожна по сравнению с массой Солнца, эта сумма практически равна массе Солнца.