Тим Глинн-Джонс - Странности цифр и чисел.

2 3= 8 3 3= 27 8 х 27 = 216

В христианстве число 666 имеет чрезвычайно важное значение, и число 216 иногда принимают как его отображение: 6 х6 х6 = 216.

Это константа в волшебном квадрате умножения 3 х 3. Произведение каждой строки, колонки и ряда по диагонали равно 216.

2 9 12

36 6 1

3 4 18

В еврейской каббале считается, что число 216 символизирует истинное имя Господа. Это было отражено в фильме «Пи» (1998 год).

216 — это самое маленькое число, которое является кубом и одновременно суммой трех чисел в кубе.

3 3+ 4 3+ 5 3= = 27 + 64 + 125 = 216

Число 220 гордится своим уникальным рекордом, так как это самое маленькое дружественное число. Его «партнер» в этом ряду — 284. Дружественные числа — это пара натуральных чисел, каждое из которых равно сумме всех правильных делителей другого (отличных от самого числа). Делители числа 220: 1 + 2 + 4 + 5 + + 10 + 11 + 12 + 20 + 22 + 44 + 55 + + 110 = 284.

Делители числа 284: 1 + 2 + 4 + 71 + + 142 = 220.

Как рассказывает легенда, один султан очень любил головоломки. Узнав, что в его тюрьме в заточении находится математик, он решил заключить с ним соглашение. Султан сказал математику, что, если тот задаст ему задачу для решения, он может гулять на свободе столько времени, сколько понадобится султану, чтобы ее решить. Однако, как только султан решит задачу, математику отрубят голову.

Тогда математик рассказал султану о паре дружественных чисел 220 и 284 и бросил ему вызов, чтобы тот нашел еще одну пару дружественных чисел. Султану так и не удалось это сделать, и математик умер в пожилом возрасте свободным человеком.

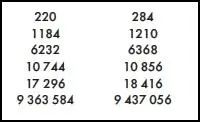
К счастью для заключенного, султан не мог воспользоваться услугами Леонарда Эйлера, швейцарского математика XVIII века, который нашел 59 пар дружественных чисел. Дружественная связь между числами 220 и 284 была известна и Пифагору, который питал к ним глубокое уважение. Считалось, что эти числа наделены особой силой, и они использовались для выражения дружественности в различных формах символизма. Но понадобилось время, чтобы кто-то смог найти другие пары таких чисел. Следующая пара — 1184 и 1210, но она была открыта только в 1866 году, когда 16-летний итальянец по имени Паганини поведал о ней миру. Эйлер и другие великие математики, такие как Декарт и Ферма, пропустили эту пару, так же как и арабский математик Аль-Банна, который нашел вторую пару, 17 296 и 18 416 (XIII столетие). Пока еще не известно, существует ли бесконечное число дружественных чисел. Пока никто не обнаружил и не доказал, что невозможно найти пару, состоящую из одного нечетного и одного четного числа. Вот несколько первых известных пар.

256 — общее число игр, которые сыграны НФЛ в сезоне, а также число знаков в 8-точечной системе Брайля, которая заменила первоначальную систему из шести точек.

256 Гц — это частота ноты до первой октавы, так любимой многими классическими композиторами. Эта частота известна как «философская», или средняя, нота до, потому что в шкале, составленной Пифагором (Пифагорейский строй), она считается самой приятной для слуха. Эта шкала была составлена с использованием простых пропорций, и Пифагор считал, что простые числа более приятны для слуха. Не зная о звуковых волнах и частотах, Пифагор составил эту шкалу, регулируя длину ряда и используя следующие пропорции.

Октава: 2 к 1; квинта: 3 к 2; терция: 5 к 4.

Однако эта система была несовершенна. В ней математически согласовались не все ноты, и поэтому между определенными клавишами образовывались дисгармоничные сочетания звуков. И люди продолжали экспериментировать с различными системами звуков, которые давали более гармоничный результат. Шкала тональностей Иоганна Себастьяна Баха была значительно совершеннее. Композитор использовал все 48 клавиш, чтобы доказать это, и написал «Хорошо темперированный клавир» (см. число 48). Это привело к развитию равномерной шкалы, в которой каждый полутон имел одинаковый интервал. Внесенное многообразие частот в музыкальное исполнение привело к бесконечным спорам на тему, каким должен быть идеальный концертный строй.

Сегодня в основе концертного строя лежит частота 440 Гц для ноты ля первой октавы. Средняя нота до попадает на частоту 261,6 Гц. Однако наблюдается сильное движение в пользу возврата к классической частоте средней ноты — 256 Гц. Именно в такой тональности написано много музыкальных произведений, поэтому певцы борются против применения более высокого строя.