Берд Киви - Книга о странном (с иллюстрациями)

Эту пирамиду (получившую краткое название D amp;M), наряду с рядом других любопытных объектов и заново переоткрытым «лицом», обнаружили на фотоснимках Марса в 1979 году компьютерщики Винсент Ди Пьетро и Грегори Моленаар, работавшие в то время в Центре космических полетов им. Годдарда. Пирамида расположена примерно в 15 километрах от «лица» и имеет пять правильных, достаточно отчетливых граней. Структура имеет весьма солидные размеры – 2,6 километра в максимальном поперечнике и около 800 метров в высоту. У основания каждого из пяти ее углов можно разглядеть не очень ясные «подпорки», что лишь усиливает впечатление об искусственном происхождении объекта.

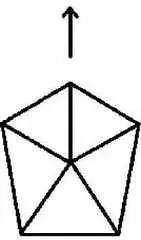
Главные же открытия необычных свойств пирамиды были сделаны в 1988-1989 годах системным аналитиком Картографического управления Министерства обороны США Эролом Торуном. Как профессионал-картограф, Торун хорошо знает геоморфологию и не сумел найти естественных объяснений для образования на поверхности планеты структуры подобной формы. Аккуратно восстановив по фотографии геометрию пирамиды D amp;M, Торун показал, что объект имеет по две пары конгруэнтных углов и осевую двустороннюю симметрию (эта ось направлена на «лицо»).

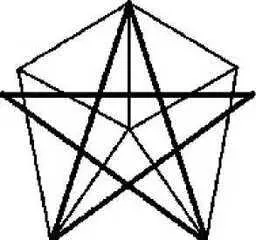
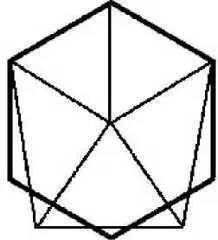
Собственно говоря, осевая симметрия и ориентация пирамиды были установлены несколькими годами ранее, в 1984 году Ричардом Хоуглендом, однако Торун продемонстрировал, что в D amp;M причудливым образом сочетаются пятикратная и шестикратная симметрии. Обе эти симметрии присутствуют одновременно, поскольку углы «фасада», обращенного к «лицу», обладают признаками 6-кратной симметричности, в то время как углы «основания» отсылают к симметрии правильной 5-конечной звезды. Но самое интересное, что в соотношении углов пирамиды D amp;M Эрол Торун обнаружил просто-таки кучу всякого рода примечательных пропорций. Поскольку пропорции носят геометрический характер, они «безразмерны» и никак не связаны с различными единицами измерения углов или сторон.

Итак, анализ показал, что на Марсе имеется чрезвычайно богатая с математической точки зрения фигура, геометрия которой включает математические основы шести– и пятиугольника, а также классические геометрические пропорции «золотого сечения». Двадцать внутренних углов модели, угловые соотношения и тригонометрические функции избыточно выражают три величины квадратных корней из 2, 3, 5 и две математические константы: число «пи» и число «е» (основание натуральных логарифмов). Причем константы появляются не одни, а в семи разных математических комбинациях.

Естественно, ошеломительные результаты Торуна поначалу вызвали у большинства ученых скепсис. Как выразился Хорас Крейтер, специалист в физике частиц и известный эксперт по преобразованию экспериментальных данных в математические структуры, сначала он «подозревал, что пропорции с подобной избыточностью могли бы случиться с разумной вероятностью в любой полусимметричной пятигранной фигуре». Многие из изученных Крейтером различных пятисторонних фигур обнаруживали пропорции, подобные соотношениям D amp;M. Увеличив точность расчетов, Крейтер к своему удивлению получил странный результат. На более высоких уровнях точности лишь модель Торуна смогла продемонстрировать столь значимый уровень избыточности.

Компьютерщик Кит Морган из Говардского университета (Вашингтон) написал специальную программу, чтобы установить перебором, какие еще пятиугольные фигуры подобного вида способны порождать такое количество математических констант. Зафиксировав два передних угла по 60 градусов, Морган прогнал ребра противоположной стороны через разные углы, получив в общей сложности 680 вариантов основания пирамидальной формы. Как показали результаты обсчета, модель Торуна является единственной пятиугольной формой с двумя углами по 60 градусов, которая выдает все эти константы, причем в таком разнообразии соотношений.