Айзек Азимов - Царство Солнца. От Птолемея до Эйнштейна

Кеплер превзошел своего учителя. Он использовал наблюдения Марса, проведенные Враге, и использовал их для того, чтобы сделать чрезвычайно важный шаг вперед в астрономии.

Иоганн Кеплер родился в 1571 г. В детстве он перенес оспу, которая изуродовала ему руки и испортила зрение. Казалось, для него оставалось только одно — стать пастором (он происходил из семьи протестантов).

В школе он учился хорошо, узнал там теорию Коперника и в конце концов оставил богословскую подготовку, чтобы стать профессором естественных наук. Однако Кеплер навсегда сохранил некий религиозный мистицизм, что сказывалось на его великих научных открытиях. Например, он уделял время разработке теорий о музыке небесных сфер.

Кеплер был также опытным астрологом и составил гороскопы многих влиятельных людей. Он немного стыдился этого, но объяснял, что это было необходимо для того, чтобы поддерживать к себе интерес власть имущих — людей, которые могли обеспечить ему поддержку и защиту в те беспокойные времена. И Кеплер, вероятно, был в этом прав, поскольку времена действительно были очень беспокойные. Также он написал великолепный научно-фантастический рассказ о путешествии на Луну, который, однако, был опубликован только после его смерти. Возможно, Кеплер стыдился и этого.

Религиозные волнения заставили его уехать из города, где он был профессором, и перебраться в Прагу, где молодой астроном присоединился к Тихо Браге. Когда вскоре после этого Тихо Браге умер, Кеплер унаследовал его место. Теперь в его распоряжении оказались все великолепные наблюдения небесных тел, которые проводил Браге, и Кеплер с энтузиазмом взялся за них. Однако эти наблюдения были не только настолько хороши, что неточная теория Птолемея к ним не подходила, — они были также слишком хороши, чтобы соответствовать теории Коперника, которая тоже оказалась недостаточно хороша.

Как Кеплер ни пытался расположить деферент и эпициклы, он просто не мог заставить свою вычисленную кривую соответствовать положению Марса, определенному Тихо. Поэтому он вынужден был сделать смелый и решительный шаг — шаг, который в чем-то был даже более смелым, чем тот, который сделал Коперник. Кеплер полностью порвал с греками!

Он отказался от окружности. Пусть она и была идеальной кривой, но она не подходила — и Кеплер ее отбросил. На самом деле сам Тихо Браге тоже думал о том, что его комета могла двигаться по некруговой орбите. Однако в то время кометы не считались достойными уважения небесными телами. От Кеплера потребовалась немалая смелость, чтобы отказаться от кругов для самих планет. Он начал искать какую-нибудь кривую, которая бы лучше, чем окружность, объясняла планетные движения. Сначала он проверил яйцевидную орбиту, но она не подошла. Затем он проверил эллипс — нечто вроде сплющенного круга.

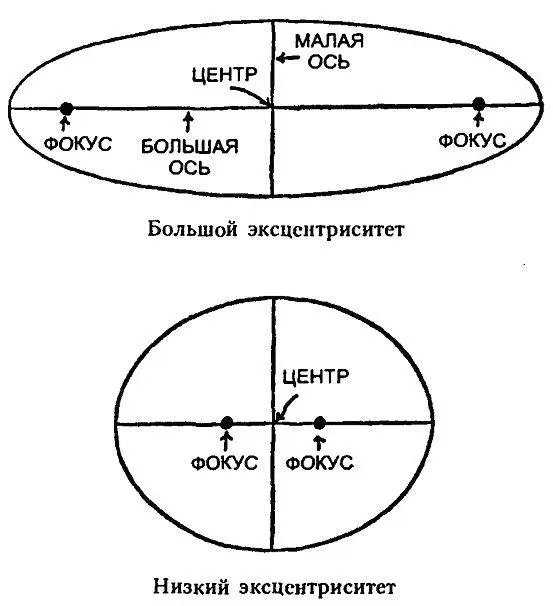
Центр круга находится на равном расстоянии ото всех точек, расположенных на окружности. Это значит, что если вы начнете от центра и проведете прямую к любой точке на окружности и обратно, то всякий раз пройдете одинаковое расстояние. Эллипс немного отличается от окружности. В нем существуют две точки, называемые фокусами. Если вы начнете отсчет из одного фокуса и будете двигаться по прямой к любой точке на границе эллипса, а потом по прямой обратно не к начальной точке, а ко второму фокусу, то пройденное расстояние всегда будет одинаковым.

Линия, проходящая через эллипс по двум фокусам, является наибольшим диаметром, который можно провести через данный эллипс. Это — большая ось. Линия, перпендикулярная большой оси и проходящая точно посередине между двумя фокусами, — это наименьший диаметр, или малая ось. Место, где эти две оси пересекаются, — центр эллипса. Два фокуса расположены по обеим сторонам от центра и на равных расстояниях от него.

Эллипс может быть широким и почти круглым или узким, сигарообразным. Чем сильнее сплюснут эллипс, тем он более эксцентричен, то есть два фокуса сильнее удалены от центра. (Как вы помните, слово «эксцентричный» происходит от греческого слова, означающего «вне центра».)

Одним из способов расчета эксцентриситета эллипса является измерение расстояния между фокусами, которое затем делится на длину большой оси. Круг можно рассматривать как эллипс, в котором два фокуса оказались настолько близки друг к другу, что совпали друг с другом и с центром. Следовательно, в круге расстояние между фокусами равно нулю. Поскольку нуль, деленный на любое число, равен нулю, то эксцентриситет круга равен нулю. С другой стороны, когда эллипс становится очень уплощенным, расстояние между фокусами все сильнее приближается к полной длине большой оси. Другими словами, эксцентриситет приближается к 1. Короче, эллипс может иметь эксцентриситет от 0 до 1.