Пекка Теерикор - Эволюция Вселенной и происхождение жизни

Таблица 23.2. Красное смещение, расстояние по времени распространения света и «расстояние сейчас».

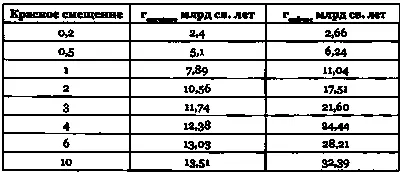
Эти расстояния рассчитаны по модели Фридмана при постоянной Хаббла = 70 км/с/Мпк, плоском пространстве, доле материи = 0,24 и доле темной энергии = 0,76.

Как пример возьмем галактику с красным смещением z = 2. Из табл. 23.2 мы видим, что свет покинул эту галактику около 10 млрд лет назад. Мы также можем вычислить, что в настоящее время она удалена от нас примерно в 7000 раз дальше, чем галактика Андромеда (расстояние до которой 2,5 млн световых лет). В этой таблице приведены расстояние по времени распространения света и «расстояние сейчас» по значению красного смещения. За единицу расстояния принят миллиард световых лет, и использована стандартная космологическая модель, в которой возраст Вселенной составляет 14 млрд лет.

Сейчас астрономы без труда наблюдают галактики до красного смещения около 0,5, что соответствует 64 % современного возраста Вселенной. С некоторыми трудностями удается наблюдать галактики при z = 3, это соответствует 16 % возраста Вселенной, а эпоха z = 10 была, когда от 14-миллиардного возраста мира прошло всего лишь 3,5 %.

Похоже, что плоские бесконечные модели Фридмана работают хорошо. Но мы хотим завершить эту главу рассказом об одном захватывающем предположении: может ли Вселенная быть плоской, но при этом конечной и содержать конечное число галактик?

Александр Фридман писал, что «распространены совершенно превратные сведения о конечности, замкнутости, кривизне и т. п. свойствах нашего пространства, которые будто бы устанавливаются принципом относительности… Я имею в виду пресловутый вопрос о конечности Вселенной, то есть о конечности нашего физического, занятого блистающими звездами пространства. Утверждают, что, найдя постоянную положительную кривизну Вселенной, можно якобы заключить о ее конечности и прежде всего о том, что прямая во Вселенной имеет «конечную длину», что объем Вселенной является тоже конечным и т. п.».

Он хотел подчеркнуть, что хотя в общей теории относительности кривизна пространства служит определяющей величиной, измерив ее, мы еще не узнаем глобальную форму и объем пространства. Отдельным вопросом является топология пространства. Напомним, что топология — это область математики, изучающая среди прочего особенности геометрических фигур и тел, которые не изменяются при растяжении или изгибе. В этом смысле, например, бублик и рамка от картины топологически эквивалентны. Так вот, топологию пространства невозможно вывести из общей теории относительности: нет простого, взаимно однозначного соответствия между кривизной пространства и его общей формой.

В процитированной выше книге «Мир как пространство и время», опубликованной в России в 1923 году, за два года до безвременной смерти, Фридман приводит педагогический пример. Двумерная геометрия поверхности цилиндра и геометрия плоскости одинаковы: обе поверхности — двумерные евклидовы пространства (рис. 23.8). Цилиндр можно склеить из плоского куска, и с нарисованным на плоскости треугольником ничего особенного не случится, если мы склеим друг с другом края этого куска. Сумма углов треугольника останется равной двум прямым углам, и теорема Пифагора, которая работает на плоскости, сохранит свою силу и на поверхности цилиндра.

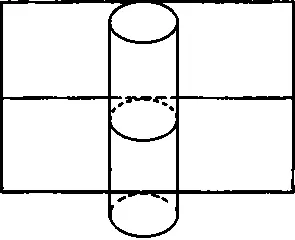
Рис. 23.8. Цилиндр можно изготовить из плоского прямоугольника. Поверхность цилиндра и плоскость обладают одинаковой внутренней евклидовой геометрией, но глобальная, то есть топологическая, структура у них совершенно разная.

Но в топологическом смысле это разные вещи: на цилиндре существуют «прямые линии конечной длины», тогда как на плоскости таких линий нет. Цилиндр имеет конечный размер в направлениях, перпендикулярных его оси, поэтому в этих направлениях он конечен и замкнут. Он бесконечен в направлении, параллельном его оси. Используя плоскость и цилиндр, Фридман приводит читателя к выводу: «Таким образом, одна метрика мира не дает нам никакой возможности решить вопрос о конечности Вселенной. Для решения этого вопроса нужны дополнительные теоретические и экспериментальные исследования».