Шинтан Яу - Теория струн и скрытые измерения Вселенной

Мы с Ченгом нашли способ решения этой задачи, и наша статья, посвященная этому вопросу, вышла в 1976 году. Как выяснилось, другое решение было представлено несколькими годами раньше — в 1971 году российским математиком Алексеем Погореловым. Ни я, ни Ченг никогда не видели его статьи, поскольку она была опубликована на родном языке Погорелова. В конце концов, все свелось к решению сложнейшего дифференциального уравнения в частных производных из тех, которые никогда до этого не решались.

Несмотря на то что никому до нас не удавалось решить проблему данного типа, за исключением Погорелова, работа которого была нам неизвестна, процедура, позволяющая работать с нелинейными дифференциальными уравнениями в частных производных, на тот момент была уже хорошо разработана. Метод работы с подобными уравнениями, получивший название метода непрерывности , был основан на использовании последовательных приближений. И хотя этот общий подход никоим образом нельзя было назвать новым, особенность состояла в том, что каждая конкретная задача предусматривала разработку своей собственной стратегии, необходимой для ее решения. Основная идея заключалась в последовательной аппроксимации решения различными функциями так, чтобы каждое следующее приближение давало результаты лучше, чем предыдущее. Суть доказательства состояла в том, чтобы показать, что после достаточно большого числа итераций приближенная функция с большой точностью совпадет с решением искомого дифференциального уравнения. В случае удачи полученное путем аппроксимации приближение нужно рассматривать не как решение дифференциального уравнения, которое можно представить в виде определенной формулы, а как доказательство того факта, что решение существует. Для гипотезы Калаби и других задач того же типа существование решения дифференциального уравнения в частных производных эквивалентно доказательству существования определенной геометрии для заданных «топологических» условий. Это не означает, что вы ничего не знаете о решении, существование которого только что доказали. Схема, которая была использована для доказательства существования решения, зачастую может быть легко преобразована в численный метод для приближенного решения на компьютере. О численных методах речь пойдет в девятой главе.

Рис. 5.1.Математик Ш. Ю. Ченг (фотография Джорджа М. Бергмана)

Метод непрерывности был назван так потому, что он подразумевает непрерывное преобразование решения некоего известного уравнения вплоть до его полного совпадения с решением искомого. Процедуру преобразования, как правило, разбивают на две части, одна из которых работает только в непосредственной близости от известного решения.

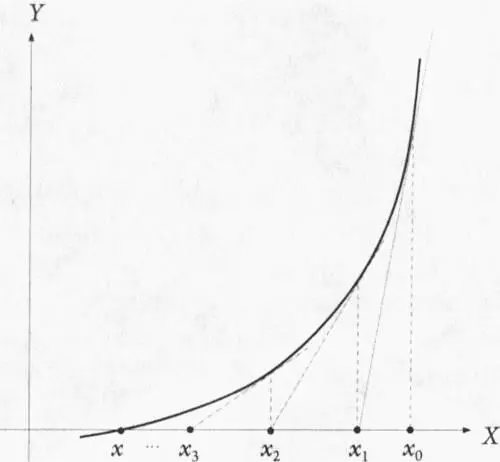
Рис. 5.2.Наглядная иллюстрация метода Ньютона. Для того чтобы найти точку пересечения определенной кривой или функции с осью X , сначала нужно наугад подобрать некую точку x 0 наиболее подходящую для этого. Затем необходимо провести касательную к кривой в точке x 0 и отметить точку, в которой эта касательная пересечет ось X (это будет точка x 1 ). В том случае, если наше изначальное предположение не было полностью ошибочным, продолжая этот процесс, мы будем получать точки все ближе и ближе к искомой

Одна из этих частей носит название метода Ньютона, так как она в определенной степени основана на методе, разработанном Исааком Ньютоном более трехсот лет назад. Для того чтобы продемонстрировать этот метод в действии, рассмотрим функцию y=x 3-3x+1 , которая описывает кривую, пересекающую ось X в трех различных точках, являющихся корнями этого полинома. Подход, предложенный Ньютоном, позволяет определить положение корней на оси X , что далеко не всегда можно сделать, просто взглянув на уравнение. Предположим, что напрямую решить уравнение нельзя, однако один из корней соответствующей функции можно найти вблизи точки x 1. Касательная, проведенная к кривой в этой точке, пересечет ось X в другой точке — x 2 , находящейся ближе к искомому корню, чем точка x 1 . Если мы проведем касательную в точке x 2 , она пересечет ось X в точке x 3 , которая будет еще ближе к искомому корню. Таким образом, многократное повторение данной процедуры должно довольно быстро привести нас к искомому корню, если только начальная точка x 1 была выбрана более-менее удачно.