5. Качественный анализ и численное решение одномерной математической модели динамики объекта
Качественный анализ итерационной системы или нелинейного дифференциального уравнения позволяет ещё до их решения определить особенности поведения моделируемой системы как нелинейного объекта не только в прошлом и настоящем, но и в будущем.
Начнём анализ с автономной итерационной системы.
Выполнение условия μ n= F( μ n) означает, что система находится в стационарном состоянии.
Стационарное состояние называется устойчивым и обозначается μ SU, если существует некоторая область (окрестность μ SU) в фазовом пространстве такая, что, как только процесс в какой-то момент времени пришел в состояние из этой области, то он начинает стремиться к устойчивому стационарному состоянию параметра целого μ SU. Если такой области нет, т. е. если микроотклонение от точки, соответствующей стационарному значению μ SU, приводит к существенным макроизменениям в течении процесса, состояние системы является неустойчивым стационарным состоянием.
В общем случае график μ 2= F( μ 1), соответствующий итерационному соотношению, иллюстрирует закон эволюции системы и позволяет определять стационарные состояния системы и их тип.
Если кривая μ 2= F( μ 1), определяемая соответствующим итерационным соотношением μ n+1= F( μ n), пересекает прямую μ 2= μ 1, в точке μ Sи |F 1( μ 1)| < 1, то μ S— устойчивая стационарная точка, а если |F 1( μ 1)| > 1, то неустойчивая. Рассмотрим подробнее математическую модель автономного дифференциального уравнения первого порядка d μ/df= f( μ). Его общее решение имеет вид.
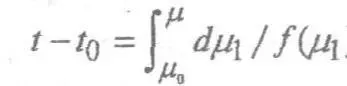
Если для какой-либо структуры в определенные моменты удалось экспериментально определить как величину выбранного нами параметра целого, так и его производной по времени, то затем, аппроксимируя функцию f( μ), например, при помощи дробно-рациональной функции 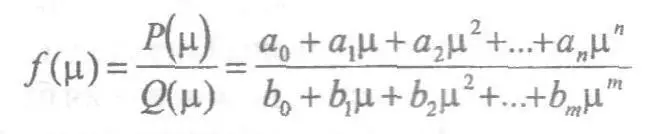
можно найти коэффициенты аппроксимации a i, b i, соответствующие экспериментальным данным.
Во многих случаях поведение системы вблизи особых точек, соответствующих нулям или полюсам функции f( μ)описывается степенной функцией с рациональным или иррациональным показателем степени или логарифмической функции. При этом появляется многозначность поведения исследуемой модели. Величины f( μ)могут одновременно с различной степенью вероятности принимать конечное или бесконечное множество действительных и комплексных значений, физический смысл которых для реальных систем должен быть специально уточнён.
Экспериментальные данные показывают, что большинство структур после периода бурного роста выходят на стабильный режим. в котором структура находится значительное время.
Этот процесс можно описать, используя квадратичную функцию f( μ).
Рассмотрим так называемое логистическое уравнение, которое было подробно изучено в связи с анализом роста и стабилизации популяций животных, однако имеет широкое применение при исследовании различных систем. Оно имеет вид d μ/dt= f(1- μ) μ.
Описываемый этим уравнением процесс имеет две стационарные точки μ=0 и μ= 1. Точка μ=0 неустойчива; это значит, что новые структуры могут появляться, в частности, при потере устойчивости старых. Точка μ=0 устойчива. Фазовая плоскость уравнения — зависимость d μ/dtот μ, представляющая собой параболу, наиболее сжато и полно характеризует особенности процесса.
В некотором смысле логистическое уравнение универсально, так как его интегральные кривые описывают процесс перехода динамической системы из одного — неустойчивого состояния в другое — устойчивое. Оно также характеризует типичный процесс роста и стабилизации структур различной природы. Его решение в случае μ< 1 имеет вид.
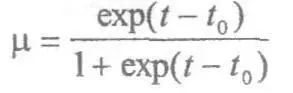
При стремлении μк нулю в момент начала роста структуры логистическая кривая асимптотически приближается к экспоненциальной. Однако, по мере увеличения меры μв структуре, описываемой этой кривой, развиваются процессы, препятствующие дальнейшему экспоненциальному росту структуры, и вблизи μ=0,5 различие кривых становится существенным. Логистическая кривая выходит на асимптоту μ= 1, а экспоненциальная кривая уходит вверх.
Читать дальше

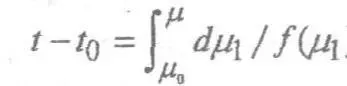
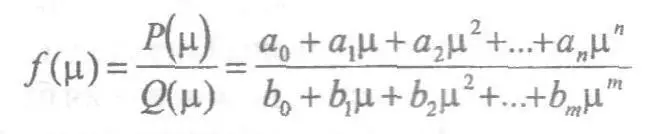
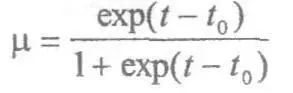






![Марианна Басина - Там, где шумят михайловские рощи [без иллюстраций]](/books/410542/marianna-basina-tam-gde-shumyat-mihajlovskie-rochi-thumb.webp)
![Марианна Басина - Далече от брегов Невы [без иллюстраций]](/books/410545/marianna-basina-daleche-ot-bregov-nevy-bez-illyustr-thumb.webp)

