Жозе Фаус - Наука. Величайшие теории - выпуск 3 - Гейзенберг. Принцип неопределенности. Существует ли мир, если на него никто не смотрит?

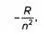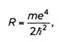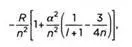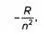
где n – главное квантовое число, R – постоянная Ридберга. Бор получил выражение

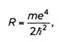
где m – масса электрона, е – его электрический заряд, h– редуцированная постоянная Планка.

В расширенной модели Зоммерфельда использовалось второе квантовое число, которое мы обозначили буквой l, принимающее значения от 1 до n. С помощью релятивистских поправок Зоммерфельд определил, что энергия стационарного состояния определяется как

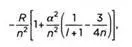
где α – постоянная тонкой структуры. Большее значение поправки, соответствующее квантовым числам n = 1 и l = 0, равняется 1 + α²/4 и равно 1,000013…, то есть примерно одной стотысячной.

Спустя несколько недель после того, как Зоммерфельд допустил Гейзенберга на свои семинары, он предложил новому студенту задачу, которую не мог решить сам. В 1895 году голландский физик Питер Зееман (1865-1943) обнаружил, что в присутствии магнитного поля некоторые спектральные линии утраиваются. Появление дополнительных линий не зависело от анализируемого вещества и определялось магнитным полем. Этот эффект можно было объяснить с помощью законов классической физики, однако ученых интересовала его интерпретация в рамках обобщенной модели атома, предложенной Зоммерфельдом. Электрон, движущийся по замкнутой орбите, эквивалентен электрическому току в катушке, который, в свою очередь, порождает магнитное поле. Это магнитное поле взаимодействует с внешним магнитным полем, при этом энергия их взаимодействия зависит от угла между ними. Зоммерфельд предположил, что этот угол также описывается квантовыми законами и может принимать только дискретные значения, определяемые неким квантовым числом. Это число Зоммерфельд назвал магнитным числом и обозначил его буквой m. Таким образом, в магнитном поле энергия стационарного состояния зависела от трех квантовых чисел: n, l, m. Далее Зоммерфельд попытался рассчитать частоты перехода на основе разности энергий и сравнить их с наблюдаемыми линиями спектра.

Его метод был корректным, однако переставал работать, когда наблюдались другие удвоенные линии, положение которых определялось не только магнитным полем, но и исходным спектром. Это явление получило название аномального эффекта Зеемана. Его объяснение Зоммерфельд и поручил Гейзенбергу. В случае классического эффекта Зеемана достаточно было описать каждое стационарное состояние с помощью трех квантовых чисел (n,l, m), рассмотрев геометрию орбит электронов. Зоммерфельд перешел к рассмотрению четвертого квантового числа, которое назвал внутренним, и попытался представить спектральные термы в виде частного целых чисел так, чтобы их разность соответствовала результатам наблюдений. После нескольких безуспешных попыток он передал задачу Гейзенбергу, который начал обучение всего несколько недель назад. Для решения проблемы юноше требовалось изучить совершенно новую в то время квантовую теорию, а также основы физики.

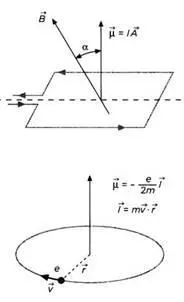
Катушка, по которой течет электрический ток, ведет себя как магнитный диполь, то есть аналогично стрелке компаса. На рисунке изображена прямоугольная катушка (впрочем, ее форма не имеет значения). Введем вектор →A, перпендикулярный плоскости катушки, длина которого будет равна площади катушки. Если через катушку течет ток силой l, дипольный момент катушки определяется как вектор →μ=l→A. Энергия взаимодействия с магнитным полем B равна скалярному произведению – →μ• →B, то есть μBcosα, где α – угол между векторами →μ и →B. Теперь рассмотрим электрон, который движется по круговой орбите радиуса r со скоростью T=2πr/v. Момент импульса электрона на орбите будет задаваться вектором →l = m→v•→r, перпендикулярным плоскости орбиты. Движение заряженного электрона по орбите будет эквивалентно электрическому току l=-е/Т в круговой катушке радиуса r. Магнитный момент будет обозначаться вектором, перпендикулярным плоскости катушки. Чтобы вычислить модуль этого вектора, нужно умножить силу тока l на площадь катушки πr² . Результат будет пропорционален моменту импульса электрона и может быть записан так: