Сергей Кургинян - Содержательное единство 2001-2006

Если в автобусе давка и вам нужно втолкнуть в него еще десяток человек, то это что значит? Что масса тел будет реагировать на новый импульс фактически по закону теории упругости. То есть передавать давление от входящих к стоящим в углах.

А если у вас есть распределение обязанностей между членами элитного сообщества и вы воздействуете на это распределение, будет ли работать та же самая "теория социальной упругости"? Конечно, будет! Не может она не сработать. И не надо для этого знать закулисные тайны. Просто иначе не может быть. А если еще точнее – то, возможно, иначе и может быть, но это маловероятно.

В любом случае, мы можем высказать определенную гипотезу. И если других гипотез нет, а эта работает, то высказанное получает статус допустимой аналитической гипотезы. И не более того. На большее я и не рассчитываю. Потому что меня в происходящем интересуют не "тайны мадридского двора", а диалектика формы и содержания. А также потому, что все, претендующее на бoльшую достоверность, чем подобные гипотезы, адресуют к тому самому "ОРЕШЬ, КАК ПАСТУХ НА ВЫПАСЕ". А значит, является для нас неприемлемым.

Итак, я буду обсуждать несколько социодинамических моделей.

Первая из них касается так называемого закона автоколебаний в системах. Предположим, что у вас есть параметр системы Х, а также время Т, в ходе которого вы меняете значение этого параметра: в начальный момент Т0 значение параметра было Х0, а в момент времени Т1 вы вдруг резко сменили это значение на значение Х1 (рис.4).

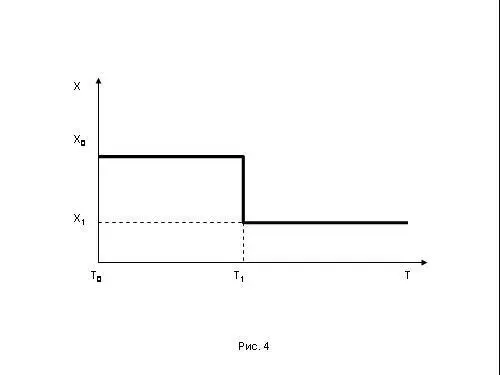
О чем говорит теория систем? Любых систем – технических, биологических, социальных… О том, что такой скачкообразной кривой Х (Т), которую мы жирно нарисовали на рисунке 4, вообще-то говоря, не может быть. То есть, в лучшем случае, мы ее можем так нарисовать на бумаге, если у нас рука не дрожит. А любая система будет реагировать на подобный переход из состояния Х0 в состояние Х1 с помощью особого колебательного механизма. Что и составляет суть так называемого переходного периода. О котором часто говорится. Но на уровне общих слов, вне реального системного содержания.

Иначе говоря, вместо скачкообразной кривой Х (Т), которую мы жирно обозначили на рисунке 4, будет иметь место примерно такая кривая (рис.5).

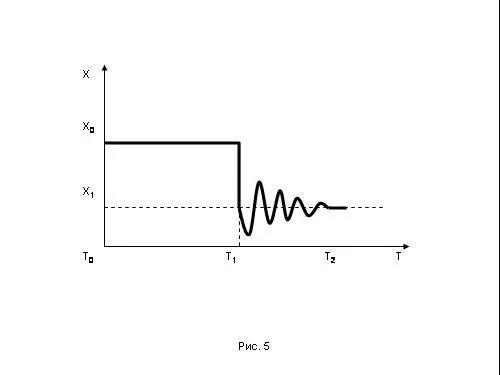
В какой-то момент Т2 система выйдет на параметр Х1. Но это произойдет не сразу. А в переходный период между Т1 и Т2 она будет колебаться в каком-то диапазоне параметра Х. Что и составляет суть переходного периода.

Причем переходный период может разворачиваться по-разному. В очень равновесных, вязких системах это будет протекать примерно так (рис.6).

А в системах, где исчерпаны вязкость и запас равновесия, процесс может, например, разворачиваться вот так (рис.7).

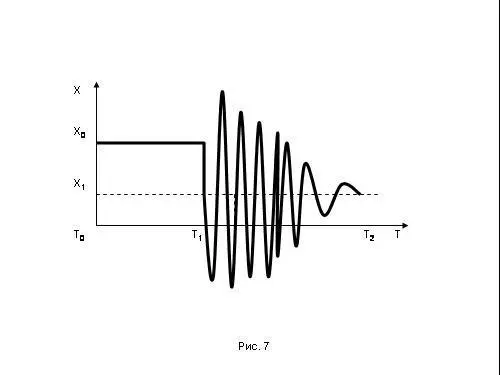
Решили вы, например, понизить плановость экономики с уровня Х0 до уровня Х1 (то есть увеличить степень рыночности хозяйства), толкнули систему в сторону Х1. А она оказалась неустойчивой. И так начала качаться, что в какой-то момент вы вместо понижения степени плановости хозяйства увеличили эту степень плановости.

Потом вы, может, и придете к нужному уровню. Но это еще когда придете! А возможно, никогда не придете. Потому что любая система обладает пределом прочности Y. За этим пределом прочности Y наступает "точка невозврата". Система перестает существовать в режиме затухающих колебаний и просто идет вразнос, куда угодно, по любой кривой (рис.8).

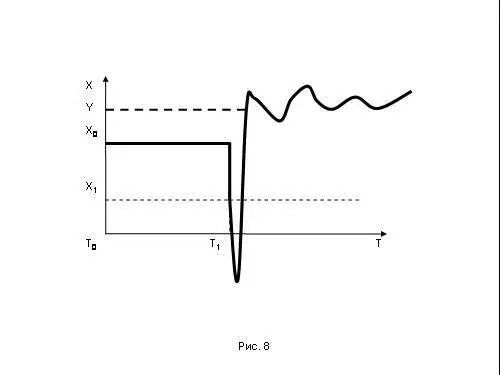
Вы можете навязать такое системное изменение, которое вроде бы должно привести систему к более хорошим параметрам. Но если система неустойчивая, то вместо этого перехода к хорошим параметрам она пойдет вразнос. И придет неизвестно куда или просто рухнет. Самый глобальный пример такого обрушения – перестройка СССР.

Но то же самое касается неизмеримо более мелких вещей. Реформирования отдельных институтов, например, армии. Административного реформирования. И чего угодно еще.