The next year, David H. Bailey, at NASA, used a Cray supercomputer and a formula discovered by two brothers, Jonathan and Peter Borwein, to scoop twenty-nine million digits of pi. Bailey found nothing unusual. A year after that, Kanada and his Tokyo team got 134 million digits of pi. They saw no patterns anywhere. Kanada stayed in to the game. He went past two hundred million digits, and saw further amounts of nothing. Then the Chudnovsky brothers (who had not previously been known to have any interest in calculating pi) suddenly announced that they had obtained 480 million digits of pi—a world record—using supercomputers at two sites in the United States. Kanada’s Tokyo team seemed to be taken by surprise. The emergence of the Chudnovskys as competitors sharpened the Tokyo team’s appetite for more pi. They got on a Hitachi supercomputer and ripped through 536 million digits of pi, beating the Chudnovsky brothers and setting a new world record. They saw nothing new in pi. The brothers responded by smashing through one billion digits. Kanada’s restless boys and their Hitachi were determined not to be beaten, and they soon pushed into slightly more than a billion digits. The Chudnovskys took up the challenge and squeaked past the Japanese team again, having computed pi to 1,130,160,664 decimal places, without finding anything special. It was another world record. At this point, the brothers gave up, out of boredom.
If a billion decimals of pi were printed in ordinary type, they would stretch from New York City to the middle of Kansas. This notion raises a question: What is the point of computing pi from New York to Kansas? That question was indeed asked among mathematicians, since an expansion of pi to only forty-seven decimal places would be sufficiently precise to inscribe a circle around the visible universe that doesn’t deviate from perfect circularity by more than the distance across a single proton. A billion decimals of pi go so far beyond that kind of precision, into such a lunacy of exactitude, that physicists will never need to use the quantity in any experiment—at least, not for any physics we know of today. The mere thought of a billion decimals of pi gave some mathematicians a feeling of indefinable horror, and they declared the Chudnoskys’ effort trivial.
I asked Gregory if an impression I had of mathematicians was true, that they spend a certain amount of time declaring one another’s work trivial. “It is true,” he admitted. “There is actually a reason for this. Because once you know the solution to a problem it usually is trivial.”
For that final, record-breaking, Hitachi-beating, transbillion-digit push into pi, Gregory did the calculation from his bed in New York, working on the Internet with the Cray supercomputer in Minneapolis, occasionally answering the phone when the system operator called to ask why the Cray had crashed. Gregory also did some of the pi work on a massive IBM dreadnought mainframe at the Thomas J. Watson Research Center, in Yorktown Heights, New York, where he also triggered some dramatic crashes. The calculation of more than a billion digits of pi took half a year. This was because the Chudnovsky brothers could get time on the supercomputers only in bits and pieces, usually during holidays and in the dead of night.
Meanwhile, supercomputer system operators had become leery of Gregory. They worried that he might really toast a $30 million supercomputer. The work of calculating pi was also very expensive for the Chudnovskys. They had to rent time on the Cray. This cost the Chudnovskys $750 an hour. At that rate, a single night of driving the Cray into pi could easily cost the Chudnovskys close to ten thousand dollars. The money came from the National Science Foundation. Eventually the brothers concluded that it would be cheaper to build their own supercomputer in Gregory’s apartment. They could crash their machine all they wanted in privacy at home, while they opened doors in the house of numbers.
When I first met them, the brothers had got an idea that they would compute pi to two billion digits with their new machine. They would try to almost double their old world record and leave the Japanese team and their sleek Hitachi burning in a gulch, as it were. They thought that testing their new supercomputer with a massive amount of pi would put a terrible strain on their machine. If the machine survived, it would prove its worth and power. Provided the machine didn’t strangle on digits, they planned to search the huge resulting string of pi for signs of hidden order. In the end, if what the Chudnovsky brothers ended up seeing in pi was a message from God, the brothers weren’t sure what God was trying to say.
* * *
GREGORY SAID, “Our knowledge of pi was barely in the millions of digits—”
“We need many billions of digits,” David said. “Even a billion digits is a drop in the bucket. Would you like a Coca-Cola?” He went into the kitchen, and there was a horrible crash. “Never mind, I broke a glass,” he called. “Look, it’s not a problem.” He came out of the kitchen carrying a glass of Coca-Cola on a tray, with a paper napkin under the glass, and as he handed it to me he urged me to hold it tightly, because a Coca-Cola spilled into—He didn’t want to think about it; it would set back the project by months. He said, “Galileo had to build his telescope—”
“Because he couldn’t afford the Dutch model,” Gregory said.
“And we have to build our machine, because we have—”
“No money,” Gregory said. “When people let us use their supercomputer, it’s always done as a kindness.” He grinned and pinched his finger and thumb together. “They say, ‘You can use it as long as nobody complains. ’”
I asked the brothers when they planned to build their supercomputer.
They burst out laughing. “You are sitting inside it!” David roared.
“Tell us how a supercomputer should look,” Gregory said.
I started to describe a Cray to the brothers.
David turned to his brother and said, “The interviewer answers our questions. It’s Pirandello! The interviewer becomes a person in the story.” David turned to me and said, “The problem is, you should change your thinking. If I were to put inside this Cray a chopped-meat machine, you wouldn’t know it was a meat chopper.”
“Unless you saw chopped meat coming out of it. Then you’d suspect it wasn’t a Cray,” Gregory said, and the brothers cackled.
“In a few years, a Cray will fit in your pocket,” David said.
Supercomputers are evolving incredibly fast. The definition of a supercomputer is simply this: one of the fastest and most powerful computers in the world, for its time. M zero was not the only ultra-powerful silicon engine to gleam in the Chudnovskys’ designs. They had fielded a supercomputer named Little Fermat, which they had designed with Monty Denneau, a supercomputer architect at IBM, and Saed Younis, a graduate student at the Massachusetts Institute of Technology. Little Fermat was seven feet tall. It sat in a lab at MIT, where it considered numbers.
What m zero consisted of was a group of high-speed processors linked by cables (which covered the floor of the room). The cables formed a network among the processors that the Chudnovskys called a web. On a piece of paper, Gregory sketched the layout of the machine. He drew a box and put an X through it, to show the web, or network. Then he attached some processors to the web.
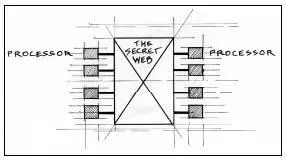
The design of the supercomputer m zero.
Drawing by Richard Preston
The exact design of this web was a secret. “Each processor is connected to all the others,” Gregory said. “It’s like a telephone network—everybody is talking to everybody else.” This made the machine very fast. They planned to have 256 processors. “We will be able to fit them into the apartment,” Gregory said. The brothers wrote the machine’s software in FORTRAN, a programming language that is “a dinosaur from the late fifties,” Gregory said, adding, “There is always new life in this dinosaur.” He said that it was very hard to know what exactly was happening inside the machine when it was running. It seemed to have a life of its own.
Читать дальше









![Shin_Stark - В подземелье я пойду, там свой level подниму X [СИ]](/books/384602/shin-stark-v-podzemele-ya-pojdu-tam-svoj-level-po-thumb.webp)



