Ханна Фрай - Математика любви. Закономерности, доказательства и поиск идеального решения

Лично для меня главным открытием стало то, что наша внешность – вовсе не определяющий фактор нашей популярности на сайте. Более того, если кто-то считает вас некрасивым, то иногда это может пойти вам на пользу.

В одном из необязательных (заполняющихся по желанию) разделов анкеты OkCupid вы можете оценить привлекательность других пользователей по шкале от 1 до 5. Чтобы оценить связь между внешностью и популярностью, команда OkCupid случайным образом отобрала 5000 пользовательниц и сопоставила среднюю оценку внешней привлекательности, которую каждая из них получила от других пользователей, с количеством полученных ею за месяц запросов.

Результаты представлены в графике. Каждый черный крестик обозначает одну пользовательницу, причем самые популярные из них сосредоточены в верхней части графика, наиболее привлекательные внешне – в правой части. На первый взгляд, крестики разбросаны по всему полю графика совершенно хаотично. Но именно эта разбросанность и есть самое интересное: она говорит о том, что не только самые красивые люди получают много сообщений.

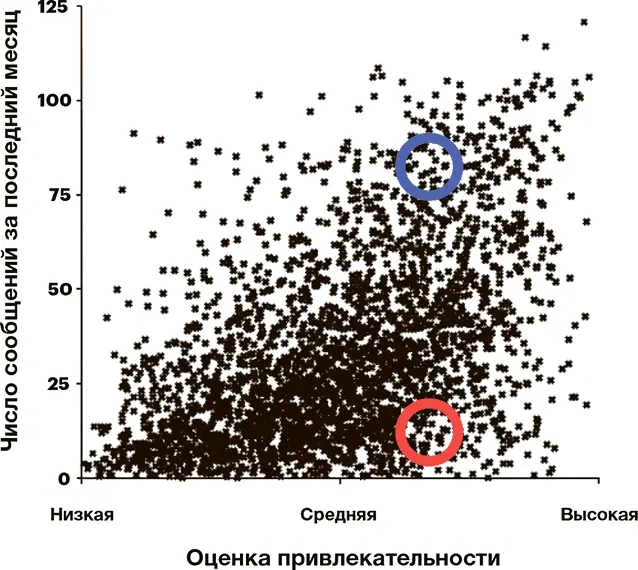
Однако если высокой оценки привлекательности недостаточно для того, чтобы добиться популярности, тогда что же еще нужно? И почему налицо такая разница в популярности между пользователями в верхней части поля (синий кружок) и в нижней (красный кружок) – притом, что у них одинаковая средняя оценка внешности?

Ответ, полученный командой OKCupid, заключается в следующем: все зависит от того, как именно люди оценивают вашу привлекательность. Лучше всего объяснить это на примере. Представьте себе двух равно очаровательных героинь мультфильмов: Вилму Флинтстоун из “Флинтстоунов” и Турангу Лилу из “Футурамы”.

Думаю, все согласятся с тем, что Вилма – красивая женщина. Никто не назовет ее уродливой, хотя она, конечно, и не дотягивает до уровня такой секс-бомбы как Джессика Рэббит – героиня еще одного мультсериала (о кролике Роджере).

Теперь сравним Вилму с красоткой Лилой. Очень многие, включая меня, считают Лилу чрезвычайно сексуальной. С другой стороны, кого-то, наверное, может отпугнуть тот факт, что у нее один-единственный глаз.

Я бы предположила, что обе женщины получат примерно одинаковую среднюю оценку. Но способы расчета этой оценки будут коренным образом различаться. Практически все “отметки” Вилмы будут группироваться вокруг цифры, а вот мнения людей, оценивших внешность Лилы, будут разбросаны в очень широком диапазоне от 1 до 5.

Любопытно, что тут важен именно разброс.

Люди, внешность которых, подобно внешности Лилы, оценивается противоречиво, в конце концов получают гораздо более высокий рейтинг на сайтах знакомств, чем такие, как Вилма, которую все оценивают как “довольно хорошенькую”.

Этот эффект становится особенно заметен, если немного поработать с данными, то есть произвести их статистическую обработку. Используя так называемый метод регрессионного анализа, команда OkCupid вывела уравнение, позволяющее предсказать, на сколько сообщений в месяц может рассчитывать пользователь в зависимости от того, как другие пользователи оценивают его (или ее) внешность:

Количество сообщений = 0.4 a 1 – 0.5 a 2 – 0.1 a 4+ 0.9 a 5+ k

Здесь a 1 – количество людей, которые оценили вашу привлекательность в 1 балл, a 2 – в 2 балла, и так далее. Последний параметр, k , характеризует вашу активность на сайте. Число перед каждым слагаемым формулы (или, научно выражаясь, коэффициент) берется непосредственно из данных и показывает, в какой степени каждая из полученных вами оценок влияет на то, сколько сообщений вы можете рассчитывать получить.

Коэффициент +0,9 перед параметром a 5означает, что из каждых ста человек, поставивших вам наивысший балл (5 из 5), примерно девяносто напишут вам в течение месяца. Тем лучше для вас.

Однако тот факт, что вам будут писать те, кто считает вас горячей штучкой, понятен. Удивительно другое: коэффициент +0,4 перед a 1говорит о том, что среди тех, кто оценил вас всего в один балл, каждый четвертый тоже собирается вам написать! Да-да, вы все правильно прочитали. Чем больше людей считают, что вы похожи на Квазимодо или на лягушку, еще не превратившуюся в принцессу, тем больше вы получите писем.

И наоборот: коэффициент –0,1 перед a 4означает, что каждая сотня оценок “4” уменьшает на десять общее количество полученных вами сообщений. То есть когда вы получаете 4 балла из 5, это фактически работает против вас.