Как и вавилонянам, грекам были известны шести десятеричные дроби, о чем упоминает Птолемей в своем «Альмагесте», однако в математических вычислениях греки использовали египетскую систему. В комментариях к трактату Архимеда Евтокий Аскалонский использует
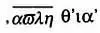
для обозначения 1838 + 1/9 + 1/11, а
для обозначения 2 + 8/11 + 8/11 + 1/99 + 1/121.
Греки и число π
Геометрия в Древней Греции находилась на очень высоком уровне развития, и грекам удалось получить более точную оценку числа π , чем их предшественникам. Архимед доказал, что число π лежит в интервале 3 + 10/71 = 223/71 < π < 3 + 1/7 = 22/7 (что соответствует среднему значению 3,141851), а Птолемей получил приближенное значение, равное 3,141666. Эти значения были получены с помощью двух правильных многоугольников (вписанного и описанного).

Гоавюры, посвященные Архимеду(слева) и Птолемею(справа).
Архимед исходил из того, что шестиугольник, вписанный в окружность единичного радиуса, имеет периметр, равный 6, а описанный шестиугольник — 4·√3. Следовательно, число π лежит в интервале от 3 до 2·√3. Он учитывал, что квадратный корень из 3 удовлетворяет следующему неравенству: 265/153 < √3 < 1351/780. Далее он перешел к правильным многоугольникам с большим числом сторон. Выбрав в качестве исходной фигуры шестиугольник, Архимед последовательно удваивал число его сторон, рассмотрев правильные многоугольники с 12, 24, 28 и 96 сторонами. С помощью правильного 96-угольника он получил приближенное значение 6336/(2017 + 1/4)< Я < 14688/(4673 + 1/2). Так как 3 + 10/71 < 6336/(2017 + 1/4) < π < 14688/(4673 + 1/2) < 3 + 1/7, он выбрал эти два значения в качестве границ интервала, в котором находится π . Птолемей рассматривал многоугольник с 360 сторонами.
Греки и простые числа
Простые числа — это натуральные числа, которые делятся только на единицу и сами на себя. Единица по определению не считается простым числом. Любое натуральное число можно представить в виде произведения простых чисел единственным образом (без учета перестановок множителей). Так, например:
120 = 5·3·2·2·2 = 2·5·2·2·3.
* * *
ПРОСТЫЕ ЧИСЛА, МЕНЬШИЕ 1000
Ниже перечислены простые числа, меньшие 1000. Они будут интересны тем, кто хочет проверить их знаменитые свойства, не затрудняя себя поиском.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
* * *
Греки изучили простые числа подробнейшим образом: они дали им определение и доказали их важнейшие свойства. Считается, что они были известны древним египтянам, однако не сохранилось никаких результатов, связанных с простыми числами, которые были бы получены предшественниками древних греков.
В 300 г. до н. э. Евклид, который работал в Александрии во времена правления Птолемея I (323–283 гг. до н. э.), в эпоху слияния египетского и греческого, обнаружил самое удивительное и важное свойство простых чисел. Он изложил его в своем трактате «Начала геометрии» — одном из важнейших трудов в истории математики. В нем заложены основы евклидовой геометрии, которая использовалась во всем мире на протяжении следующих двух тысяч лет. В предложении 20 книги IX «Начал» доказывается, что простых чисел бесконечно много.
Евклид рассматривает множество простых чисел S = { р 1, р 2 …, р n } и показывает, что число N = p 1 · р 2 ·… · р n + 1 не делится на р 1 , поскольку при делении на p 1 остаток равен 1. Аналогично N не делится на р 2 …., р n , так как при делении N на р 2 …, р n остаток будет равен 1. Следовательно, N либо простое, либо является произведением простых чисел, не содержащихся в S . Таким образом, множество S не содержит в себе все простые числа. Так как S было выбрано произвольно, конечного перечня простых чисел не существует. Как следствие, перечень простых чисел бесконечен.
Читать дальше

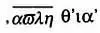







![Джонатан Макмиллан - Конец банковского дела [Деньги и кредит в эпоху цифровой революции]](/books/408207/dzhonatan-makmillan-konec-bankovskogo-dela-dengi-thumb.webp)
![Жорж Вигарелло - История тела Том 2 [От Великой французской революции до Первой мировой войны]](/books/412945/zhorzh-vigarello-istoriya-tela-tom-2-ot-velikoj-fran-thumb.webp)
![Мишель Перро - История частной жизни Том 4 [От Великой французской революции до I Мировой войны]](/books/413881/mishel-perro-istoriya-chastnoj-zhizni-tom-4-ot-velik-thumb.webp)
![Коллектив авторов История - История гражданской войны в СССР. Том 2 [Великая пролетарская революция (октябрь - ноябрь 1917 года)]](/books/420167/kollektiv-avtorov-istoriya-istoriya-grazhdanskoj-vojny-v-sssr-tom-2-velikaya-proletarskaya-revolyuciya-oktyabr-noyabr-1917-goda-thumb.webp)

