
Шестой лад состоит из двух групп по шесть звуков (тон — тон — полутон — полутон) и допускает шесть транспозиций.
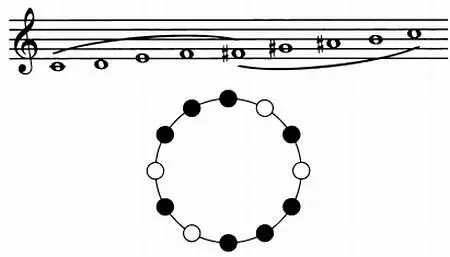
Седьмой лад состоит из двух групп по шесть звуков (полутон — полутон — полутон — тон — полутон) и допускает шесть транспозиций.
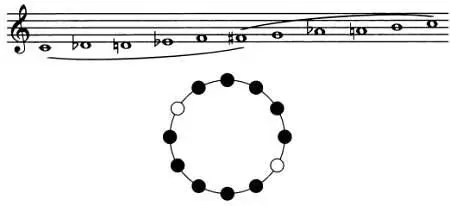
Математика музыкальной формы
Симметрия наблюдается не только в музыкальных фразах и мотивах. Более сложные музыкальные структуры также могут обладать интересными математическими свойствами.
В формальном анализе музыкальных произведений изучается «музыкальная плоскость» — иными словами, составные части произведения и взаимосвязи между ними. Так как «музыкальную плоскость» можно изображать с разной степенью точности, в зависимости от «масштаба» можно получить общее представление, не содержащее нюансов, либо, напротив, в подробностях увидеть все детали, но не все произведение в целом.
ABCDE…
Рассмотрим музыкальные произведения издалека. Мы увидим крупные структуры, которые будем обозначать заглавными латинскими буквами. Здесь в качестве структурных элементов композиции мы будем рассматривать повторяющиеся или изменяющиеся фрагменты произведения. Композицию, в которой полностью повторяется единственная группа, будем обозначать так:
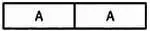
Такие композиции обладают простой симметрией. Произведение, состоящее из двух полностью различных групп, напротив, не обладает какой-либо симметрией:
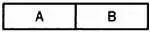
Существуют ли произведения, симметричные с формальной точки зрения? Да, такие произведения существуют, более того, они встречаются очень часто. Примером может служить скерцо («игра») — произведение, которое обычно является частью другого, более крупного произведения, например симфонии. В качестве примера можно привести скерцо из Девятой симфонии Бетховена или скерцо из Симфонии № 4 Чайковского. По своей сути скерцо имеет вид АВ . Иногда после исполнения второй части первая повторяется заново, и композиция принимает вид:

Это простейшая симметричная фигура. Части этой композиции могут повторяться и далее, образуя различные симметричные структуры:

Также существуют сложные формы, состоящие из трех частей, каждая из которых также делится на три части. В результате образуются более крупные симметричные структуры:

Некоторые короткие произведения, например вальс ор. 34 № 1 Фредерика Шопена(1810–1849) , обладают еще более широкой симметрией:

Чем длиннее произведение, тем меньше вероятность наличия подобной симметрии. «Музыкальное приношение» Баха обладает формальной симметрией следующего вида:

Месса си минор Баха
Иоганн Себастьян Бах, самый изобретательный композитор всех времен, использовал в своих произведениях структуры, обладающие символическими и математическими свойствами. Его Месса си минор (Высокая месса) BWV 232, состоит из 27 частей, объединенных в четыре группы: Kyrie, Gloria, Credo и финальную, включающую в числе прочих части Sanctus, Hosanna, Benedictus и Agnus Dei . Композитор хотел изобразить Святую Троицу как в музыке, так и в числах.
Число 3 обозначает Святую Троицу. Общее число частей произведения (27), а также число частей в каждой группе (3 + 9 + 9 + 6) делится на три. Две центральных группы ( Gloria и Credo ) имеют симметричную структуру. Центр симметрии Gloria расположен в хоре Domine Deus («Господи Боже»). Центр симметрии Credo — в Crucifixus («Распятье»):
Читать дальше






















