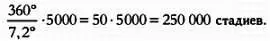Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

* * *

Кроме того, Эратосфен учел, что через Сиену проходит Северный тропик, то есть в полдень в день летнего солнцестояния (примерно 21 июня) солнечные лучи падают на город вертикально. Любой житель и гость Сиены мог подтвердить, что в этот день лучи солнца освещали глубокие колодцы до самого дна.

Схематичное изображение Александрии, Сиены и солнечных лучей, освещающих эти города в день летнего солнцестояния. Эратосфенпри измерении размеров Земли использовал похожую схему.

Чтобы измерить угол, определяемый дугой меридиана, Эратосфен также использовал гномон — простой инструмент, представляющий собой вертикальный столб, перпендикулярный горизонтальному основанию. Рассказывают, что в качестве гномона ученый использовал большой обелиск.

С помощью гномона Эратосфен измерил угол наклона Солнца относительно вертикали в полдень в день летнего равноденствия. По его подсчетам, этот угол составил 1/50 окружности, то есть 360°/50 = 7,2°. А поскольку в полдень этого же дня лучи Солнца падают на Сиену вертикально, угол дуги меридиана между Александрией и Сиеной равен α , то есть 7,2°.

* * *

ПОЛЕЗНЫЕ СВОЙСТВА ГНОМОНА

Зафиксировав гномон в одном положении, мы можем наблюдать движение его тени по мере того, как солнце движется по небу. Так, можно определить, когда наступает полдень — в этот момент Солнце находится в наивысшей точке над горизонтом, а тень гномона будет самой короткой. Гномон можно использовать и в качестве простого компаса, так как в полдень его тень указывает направление «север — юг».

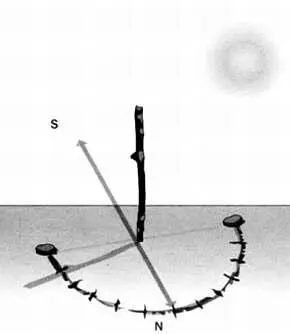
В полдень, когда длина тени гномона наименьшая, он указывает направление «север — юг». В течение дня тень гномона описывает гиперболу, симметричную относительно направления «север — юг», за исключением 20 марта и 22 сентября, — в эти дни тень гномона движется по прямой, указывающей направление «запад — восток».

Если мы будем наблюдать за гномоном, расположенным на одном и том же месте, в течение года, то сможем также определить дни летнего и зимнего солнцестояния. Если в каждый день года мы будем отмечать конец тени в полдень, то увидим, что зимой, когда Солнце находится ниже всего над горизонтом, тени будут длиннее, чем в остальные времена года. День зимнего солнцестояния — это день, когда тень гномона будет самой длинной. День года, когда тень гномона будет самой короткой, — это день летнего солнцестояния.

Гномон также можно использовать для определения угловой высоты Солнца. Чтобы измерить угол, определяющий высоту Солнца (см. рисунок ниже), нужно всего лишь измерить длину гномона и его тени. Говоря современным языком, соотношение между длиной гномона и его тени будет равно тангенсу искомого угла. Аналогично можно определить угол между гномоном и лучами Солнца, указывающий, насколько Солнце отстоит от вертикали. Этот угол будет дополнительным к первому, то есть сумма этих углов будет равна 90°.

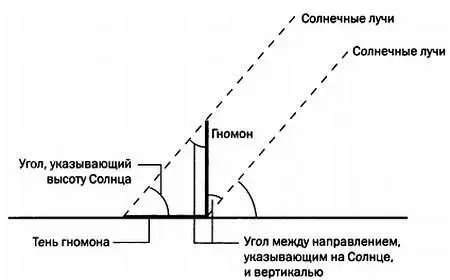
Гномон и его тень позволяют определить угловую высоту Солнца.

* * *

Путем несложных рассуждений можно прийти к выводу: если дуга меридиана имеет длину в 5000 стадиев и ей соответствует угол в 7,2°, то длина полной окружности, то есть 360°, будет равна

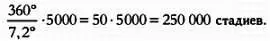
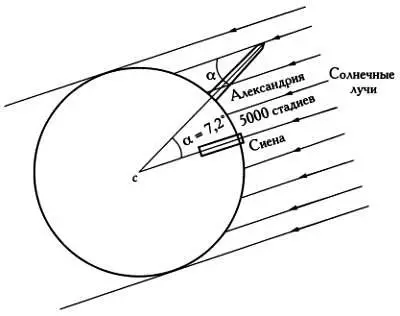
В полдень, в день летнего солнцестояния, лучи Солнца освещают Сиену вертикально, достигая дна самых глубоких колодцев. В этот же день и час лучи Солнца освещают Александрию под углом 7,2° относительно вертикали.

По-видимому, Эратосфен провел несколько измерений и в итоге получил окончательный результат в 252 тысячи стадиев. Его метод, который можно использовать и в наши дни, очень прост и эффективен. К сожалению, мы не можем точно перевести стадии в привычные нам метры: во времена Эратосфена не существовало единой системы мер, поэтому в точности неизвестно, какой была длина стадия, использованного ученым. Если мы рассмотрим египетский стадий, равный 157,5 м, то результат Эратосфена составит 39690 км. Эта цифра очень близка к 40030,2 км — именно столько составляет длина окружности Земли в сферической модели (полученной на основе эллипсоида WGS 84).