Антонио Лизана - Если бы числа могли говорить. Гаусс. Теория чисел

Многие другие записи, которые на несколько десятилетий оказались сокрытыми в этом дневнике от всех, будучи опубликованными, возвысили бы полдюжины математиков. Некоторые открытия Гаусса не были опубликованы в течение его жизни, но он не претендовал на первенство, обнаружив, что его открытия заново сделаны другими авторами, поскольку был слишком гордым, чтобы вступать в споры такого рода. Говоря о себе, Гаусс замечал, что вел научные исследования только в ответ на собственные природные устремления, а публикация результатов и приобщение к ним других людей для него всегда имели второстепенное значение.

Гаусс случайно сообщил одному из своих друзей идею, которая может объяснить как существование его дневника, так и медлительность в публикации новых результатов. Ученый утверждал, что когда ему было 20 лет, то количество новых идей, приходивших ему в голову, было таким, что он едва успевал записывать их в полном виде, и у него для таких записей было очень мало времени, поэтому в дневнике содержится только краткое изложение результатов сложных исследований, которые порой продолжались по нескольку недель. В молодости Гаусс восхищался рядом синтетических доказательств, объединявших идеи Архимеда и Ньютона, и он решил следовать великому примеру этих гигантов и оставлять только совершенные и законченные работы, к которым нельзя ничего добавить и от которых нельзя ничего отнять, не изменив их. Работа сама по себе должна быть законченной, простой и убедительной, такой, чтобы нельзя было найти какого-либо знака, указывавшего на труды, которых она стоила. Собор, говорил математик, не собор, пока не разобраны последние леса. Стремясь к этому идеалу, Гаусс предпочитал долго отполировывать свой шедевр, вместо того чтобы публиковать полный ход своих рассуждений, что он очень легко мог бы сделать. На личной печати ученого изображено дерево с небольшим количеством фруктов и девиз Pauca sed matura («Мало, но спелые»). И эти слова в точности отражали мнение Гаусса относительно научных публикаций. Как мы позже увидим, дневник помог разрешить некоторые споры, в частности возникшие с Лежандром.

Построение с помощью линейки и циркуля, до этого много раз описанное в математических работах, состоит в том, чтобы строить точки, отрезки и углы, пользуясь исключительно идеальными линейкой и циркулем. Предполагается, что линейка имеет бесконечную длину и лишена делений, позволяющих измерять и переносить расстояния, а циркуль закрывается каждый раз, поднявшись над листом бумаги, так что его также невозможно использовать для переноса расстояний, поскольку он «забывает» о расстоянии между точками, как только перестает чертить окружность. Это правило построений было введено еще древнегреческими геометрами, и с тех пор оно осталось неизменным. Ограничение для циркуля кажется очень неудобным для современных циркулей, но на самом деле не предполагает серьезных неудобств, потому что перенос расстояний можно осуществить непрямым способом, хотя и с помощью большего количества шагов. Благодаря этому правилу построение шестиугольника с помощью линейки и циркуля кажется тривиальным (поскольку каждая окружность содержит вписанный шестиугольник со стороной, равной радиусу окружности), но требует больше работы, чем могло бы показаться.

Построение шестиугольника с помощью линейки и циркуля по описанным ранее правилам показано на рисунке.

Проведем две параллельные вертикальные прямые и третью, перпендикулярную им. Проведем окружности радиусом АВ с центрами в точках А и В. Возьмем одну из точек пересечения, например О. Это центр шестиугольника. Теперь проведем окружность с центром в точке О и радиусом ОА. Получаем точки Р и Q в местах пересечения с предыдущими окружностями и точки R и S в местах пересечения вертикальных прямых с окружностью, которую мы только что провели. Соединив вершины, получаем искомый правильный шестиугольник.

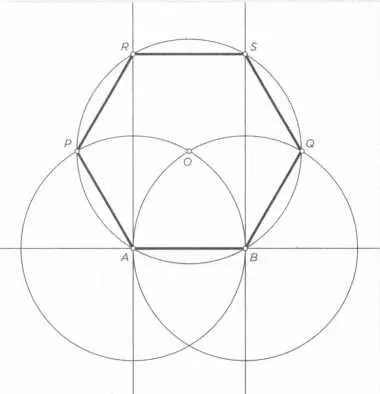
Построение шестиугольника с помощью идеальных линейки и циркуля, по традиции древних греков. Гаусса привлекло построение этих фигур, и в 19 лет он доказал, что таким образом можно нарисовать правильный многоугольник с 17 сторонами.

После того как мы определили правила, сформулированные древними греками, возникает вопрос: можно ли построить с помощью линейки и циркуля любой правильный многоугольник? Это зависит от того, о каком многоугольнике мы говорим. На основе построения шестиугольника тривиальным является построение равностороннего треугольника, поскольку для этого нужно лишь соединить чередующиеся вершины. Другая классическая проблема построений с помощью линейки и циркуля заключается в том, чтобы провести биссектрису угла. Сочетая эти два процесса, мы можем утверждать, что можно построить, по крайней мере в теории, все правильные многоугольники с числом сторон 3 х 2n, где n — натуральное число. Так, для n = 2 мы получаем 12-угольник, или многоугольник с 12 сторонами, а для n = 3 — многоугольник с 24 сторонами, и так мы можем продолжать, просто увеличивая п. Это решение очень далеко от общего ответа на вопрос. И мы увидим, что это частный случай предложенного Гауссом решения.