Хоакин Наварро - Том 31. Тайная жизнь чисел. Любопытные разделы математики

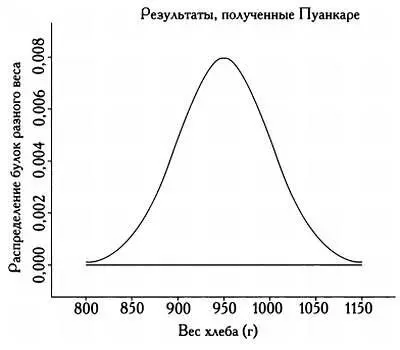
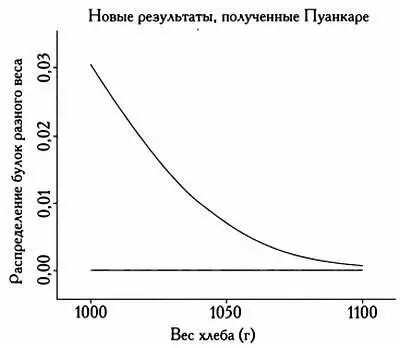
И действительно, на новой кривой распределения, построенной ученым, было видно, что теперь булочник присылал ему только булки из правой части кривой, то есть весом более 1 килограмма. Кривая четко показывала, что Пуанкаре получал только булки, которые были тяжелее обычных, а булки меньшего веса, находившиеся с другой стороны кривой нормального распределения, доставались другим покупателям. Видите, как непросто обмануть статистика!

И сэр Уильям Роуэн Гамильтон(1805–1865) , и Имон де Валера(1882–1975) были ирландцами, однако если Гамильтон был английским подданным, то де Валера стал президентом независимой Ирландии и, разумеется, обладателем ирландского паспорта. Их объединяла не только общая родина, но и любовь к математике.

Гамильтон потратил много лет на поиски алгебраического поля, которое стало бы обобщением комплексных чисел, и его поиски в конце концов увенчались успехом: в 1843 году он открыл кватернионы.

Кватернионы представляют собой сочетания символов вида

a · 1+ b · i + c · j + d · k

(обычно они записываются без единицы — a + b·i + c·j + d·k, где а, Ь, с и d — вещественные числа, 1 — единица, операция умножения является дистрибутивной, а также выполняется следующее условие: х 2= j 2= k 2= ijk = —1. Таблица умножения 1, i, j и k выглядит так:

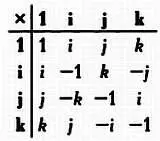
Множество кватернионов образует поле, которое заключает в себе комплексные числа (достаточно рассмотреть кватернионы при с = d = 0). По легенде, идея о кватернионах пришла в голову Гамильтону, когда он проходил по мосту Брум Бридж в Дублине.

Это открытие показалось всем столь удивительным и столь подлинно ирландским, что много лет спустя Имон де Валера возглавил церемонию открытия памятной таблички на этом мосту. На табличке было написано:

«Здесь на прогулке, 16 октября 1843 года, сэр Уильям Роуэн Гамильтон, во вспышке гения, открыл формулу умножения кватернионов х 2= j 2= k 2= ijk = —1, записав ее на камнях этого моста».

На этом история закончилась бы, если бы Имон де Валера (для друзей — Дев) не изучал математику и сам не был математиком. В 1913 году он предложил свою кандидатуру на должность преподавателя математики, но его не утвердили, хотя Артур Конвей, один из его преподавателей, говорил, что претендент «глубоко разбирался в теме». Когда в 1916 году де Валера находился в тюрьме, ожидая расстрела, то в ночь перед расстрелом он с гордостью написал на стене камеры вместо эпитафии:

х 2= j 2= k 2= ijk = —1

Любить математику больше, чем он, и вправду сложно. В конце концов де Валера спасся, занялся политикой, и математика потеряла специалиста по кватернионам, однако политика от этого только выиграла. Он пережил войну (единственным опрометчивым его шагом стало выражение соболезнований Германии в связи со смертью Гитлера) и стал президентом независимой Ирландии.

Памятная табличка на мосту Брум Бридж.

Теория множеств составляет важную часть фундамента всей математики, однако попытки преподавать ее в школах вызвали массу разногласий и споров, которые в конце концов по большей части удалось разрешить. Сегодня никто не спорит с тем, что теория множеств занимает центральное место в изучении науки, однако в начале XX века эта дисциплина, созданная благодаря усилиям Георга Кантора(1845–1918) и Рихарда Дедекинда(1831–1916) , не вызвала большого интереса в академических кругах. В Принстонском университете был организован совет ученых с целью обсуждения программы преподавания математики. Предметом этой истории, которую рассказал физик и математик Фримен Дайсон(род. 1923) , стал разговор между астрономом сэром Джеймсом Хопвудом Джинсом(1877–1946) и специалистом по топологии Освальдом Вебленом(1880–1960) . Учебная программа казалась несколько перегруженной, и Джинс предложил облегчить ее: «Мы могли бы исключить теорию множеств — в конце концов, этот раздел математики никогда не будет особенно важным для физиков», — сказал он. Однако сэр Джеймс оказался плохим провидцем, и это подтвердят те, кто изучает квантовую механику и повсеместно использует множества.