Саймон Сингх - Симпсоны и их математические секреты

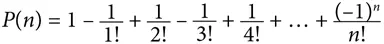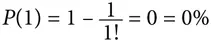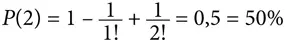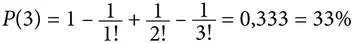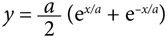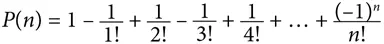
Таким образом, в случае одного посетителя вероятность отсутствия совпадений составляет 0, поскольку одна шляпа неизбежно попадет к своему владельцу:

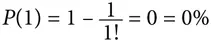
В случае двух посетителей вероятность отсутствия совпадений равна 0,5:

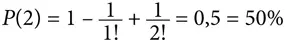
В случае трех посетителей вероятность отсутствия совпадений составляет 0,333:

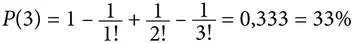
Для четырех клиентов вероятность равна примерно 0,375, а для десяти – около 0,369. Если количество клиентов стремится к бесконечности, значение вероятности становится 0,367879…, что составляет 1/2,718…, или 1/ e .

Вы можете сами проверить эту закономерность, взяв две колоды карт и перетасовав их по отдельности, чтобы карты в каждой колоде располагались произвольным образом. Одна колода символизирует случайный порядок, в котором шляпы укладывались в коробки, а другая – случайный порядок, в котором клиенты возвращались за своими шляпами. Положите обе колоды рядом друг с другом и переворачивайте по одной верхней карте в каждой колоде. Если обе карты имеют одинаковую масть и значение, это засчитывается как совпадение. Вероятность отсутствия совпадений после просмотра всех карт обеих колод близка к 1/ e , что составляет примерно 0,37, или 37 процентов. Другими словами, если вы будете повторять весь процесс сотню раз, то вас ждет не слишком активная светская жизнь и примерно тридцать семь колод карт с отсутствием совпадений. Хотя задача о шляпах может показаться тривиальной, она представляет собой фундаментальный вопрос такой области математики, как комбинаторика .

Число e также появляется в процессе изучения кривой особого типа, известной под названием катенарная кривая [43], поскольку она имеет форму цепи, провисшей между двумя точками. Этот термин, придуманный Томасом Джефферсоном, происходит от латинского слова catena , что означает «цепь». Форма катенарной кривой описывается следующим уравнением, в котором присутствует два числа e :

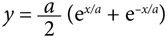
Шелковая нить в паутине образует ряд катенарных кривых между лучами паутины, что подтолкнуло французского энтомолога Жана Анри Фабра написать в книге The Life of the Spider («Жизнь пауков») следующее: «Здесь снова появляется похожее на абракадабру число e , начертанное на нитях паутины. Давайте посмотрим туманным утром, какая сетчатая структура была создана за ночь. Липкие нити, имеющие гидрометрические свойства, провисают под тяжестью крохотных капель воды и образуют множество катенарных кривых – нитей прозрачных жемчужин, изящных бус, расположенных в изысканном порядке и повторяющих форму кривой качания. Когда солнечные лучи пронизывают пелену тумана, все это начинает светиться разноцветными огнями и напоминает сверкающие нити бриллиантов. Это и есть число e во всем своем великолепии».

Мы можем также обнаружить присутствие числа e в совершенно другой области математики. Представьте себе, что вы на калькуляторе (если он достаточно «продвинутый») генерируете случайные числа от 0 до 1, а затем непрерывно суммируете их до тех пор, пока сумма не превысит единицу. Иногда вам понадобится два случайных числа, в большинстве случаев – три, время от времени – четыре или более, для того чтобы общая сумма превысила 1. Однако в среднем количество необходимых случайных чисел составляет 2,71828, а это, разумеется, и есть число e .

Существует еще много примеров, демонстрирующих, что число e играет массу разноплановых и фундаментальных ролей в разных областях математики. Это объясняет, почему любители чисел испытывают особую эмоциональную привязанность к числу e .

Один из таких поклонников – Дональд Кнут, почетный профессор Стэнфордского университета и подобная Богу фигура в мире информационных технологий. После написания Metafont (программного обеспечения для создания шрифтов) Кнут решил выпускать обновленные версии этого ПО под номерами, связанными с числом e . Это означает, что первая версия называлась Metafont 2, затем Metafont 2.7, затем Metafont 2.71 и так далее, вплоть до текущей версии Metafont 2.718281. Номер каждой новой версии представляет собой более точное приближение истинного значения числа e . Это только один из способов, с помощью которых Кнут выражает свой необычный подход к работе. Еще один пример – предметный указатель его фундаментального труда The Art of Computer Programming (том 1) [44], в котором запись «круговое определение» отсылает читателя к записи «определение, круговое», и наоборот.