Амир Фаткуллин - Сказки дедушки Амира по геометрии

Сказка о начале всех начал – о Точке

В начале было… Нечто… и – больше ничего.

Кругом была пустыня и не было того,

Кто мог бы дать названье тому,– что ж это было,

Но Нечто всё, что видим вокруг мы,– сотворило.

Котов Л. Ф.

Жила-была Точка. Вы думаете, что точка, и все – конец предложения и сказке? Нет, это не та точка, которая в конце предложения, а это -математическая Точка.

А где математическая Точка жила? Ее можно встретить на линии в одномерном пространстве, в котором есть только длина. Ее можно встретить на плоскости в двумерном пространстве, в котором есть длина и ширина. Точку можно встретить в трехмерном пространстве, где есть длина, ширина и высота.

А можно встретить Точку в четырехмерном пространстве, где уже 4 измерения? Об этом поговорим позже. Точку нельзя измерить, ведь она безразмерная, у нее нет длины, ширины, высоты, то есть Точка – это и есть Нечто.

А из этого Нечто все и появилось.

А что такое Точка? Есть синонимы Точки – это пункт, узел, позиция, пик, вершина. Часто мы слышим словосочетания: из пункта А в пункт Б… или выдвинуться на такую-то позицию…, или узловая точка, или вершина пирамиды, или пик Победы.

Когда мы смотрим на самолет вдалеке, то видим точку, но это не математическая Точка, а физическая точка. Звезды тоже мы видим в виде физических точек. А в письме – сколько грамматических точек: точка в конце предложения, двоеточие, многоточие, точка с запятой. Об этих точках будут другие сказки. А теперь уберем фамилию и будем математическую Точку называть просто Точка.

– Профессор, что такое Точка?

– Это прямая, если смотреть ей в торец.

В математике Точку называют нульмерным пространством.

А теперь начинается сказка о Точке.

Собственно она сама представляла собой пространство, только нульмерное и больше никого не было в этом пространстве. Точке стало скучно в этом нульмерном пространстве и она стала искать другие Точки. Где-то еще жили другие Точки в своих нульмерных пространствах. Но чтобы до них дойти надо попасть в другое пространство. И вот, наша Точка решила путешествовать по другим пространствам.

Она вырвалась из своего нульмерного пространства и попала в одномерное пространство. Поскольку там была длина, то она решила расти в одну сторону – и получился Луч. Так его назвала Точка, потому что он как луч света выходит из источника (Точки). Потом она решила расти в противоположную сторону – и получилась Прямая. Так ее назвала Точка за то, что она идет прямо, не отклоняясь в стороны и не останавливаясь. По пути ей встретилась другая Точка, ведь она была не единственной путешественницей, – и получился Отрезок, то есть часть прямой.

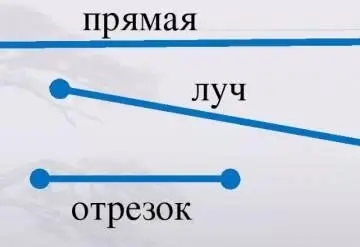
Таким образом, Точка создала в одномерном пространстве: Прямую, которая бесконечна в обе стороны, то есть не имеет ни начала ни конца. Луч – Часть прямой ограниченной с одной стороны. Отрезок – часть Прямой, ограниченной с обеих сторон.

Пока одна Точка создавала Луч, Прямую в одномерном пространстве, другие Точки тоже решили побывать там. Они как раз попали на Прямую и образовали несколько Отрезков.

Точки подружились между собой и с Отрезками и решили путешествовать вместе. Отрезки вместе с Точками вырвались в двумерное пространство.

Там Отрезки стали сравниваться друг с другом, ведь у них была длина. Потом Отрезки стали перемещаться по плоскости и пересекаться друг с другом. Что интересно, когда они пересекались, то в месте их пересечения появлялась Точка, которая как бы склеивала отрезки под каким-то углом. Таким образом, Точки появились и в двумерном пространстве.

Иногда Отрезки так располагались друг относительно друга, что не пересекались.

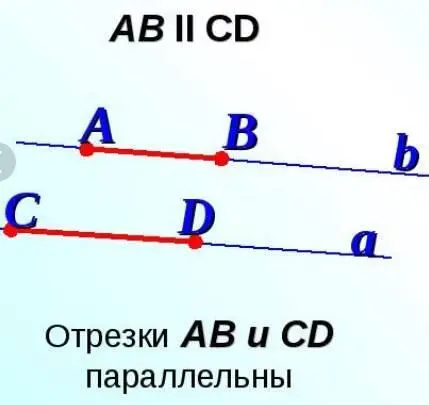
Точки стали искать причину, почему Отрезки не пересекаются, вставали в конце отрезков и увеличивали их длину, образуя лучи на продолжении Отрезков. Некоторые Отрезки действительно пересекались и образовывали между собой какой-то угол, если Точки увеличивали их длину. А некоторые Отрезки никак не хотели пересекаться на плоскости. Тогда их назвали параллельными. Но все-таки любые лучи пересекаются, но это уже в другой геометрии и другом пространстве, например, на сфере.