Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Математики делают еще один концептуальный шаг. Мы не просто следуем заранее заданным правилам — мы изобретаем их и заигрываем с ними. Мы делаем предположение, выводим его логические следствия — и если они ведут в никуда или, что гораздо хуже, если они наводят скуку, мы ищем новый и более плодотворный путь.

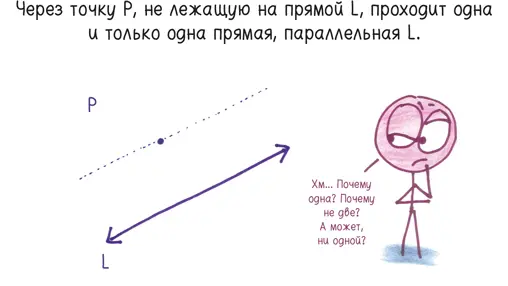
Например, что произойдет, если я усомнюсь в постулате о параллельных прямых?

Евклид изложил этот закон параллельных прямых примерно в 300 году до н. э.; он принял его как должное и назвал фундаментальным предположением («постулатом»). Его преемники сочли это несколько смехотворным. Мы действительно должны принимать на веру данное утверждение? Может быть, его можно доказать? На протяжении двух тысячелетий ученые ковыряли это правило, как волоконце мяса, застрявшее между зубов. В конце концов они поняли: «О да! Это всего лишь предположение». Вы можете предположить иное. В таком случае традиционная геометрия обрушится и уступит место диковинным альтернативным геометриям, где слова «параллельность» и «прямая» имеют совершенно другой смысл.

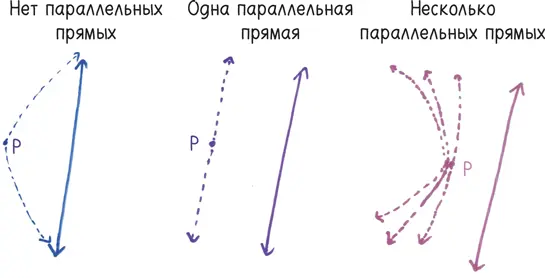
Новое правило — новая игра.

То же самое работает в случае с жесткими крестиками-ноликами. Вскоре после того, как я стал пропагандировать эту игру, я увидел единственную техническую деталь, на которой все держится. Она сводится к вопросу, которого я уже касался раньше. Как быть в том случае, если мой противник перенаправляет меня на мини-поле, которое уже сыграно?

Сейчас мой ответ совпадает с тем, который я приводил выше. Если мини-поле уже сыграно, вы можете выбрать любое другое.

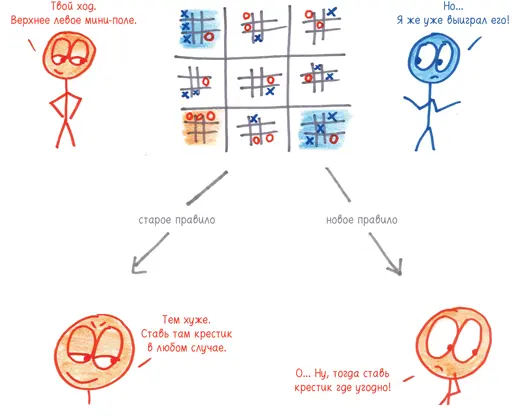
Но изначально мой ответ был другим. До тех пор, пока на этом мини-поле остаются пустые клетки, вам необходимо идти туда и делать ход, даже если он лишен смысла.

Это кажется мелочью — всего лишь одна нить в гобелене игры. Но посмотрите, как вся ткань распустится, если потянуть за нее.

Я покажу суть старого правила с помощью дебютной стратегии, которую я окрестил (в порыве скромности) «гамбитом Орлина»:

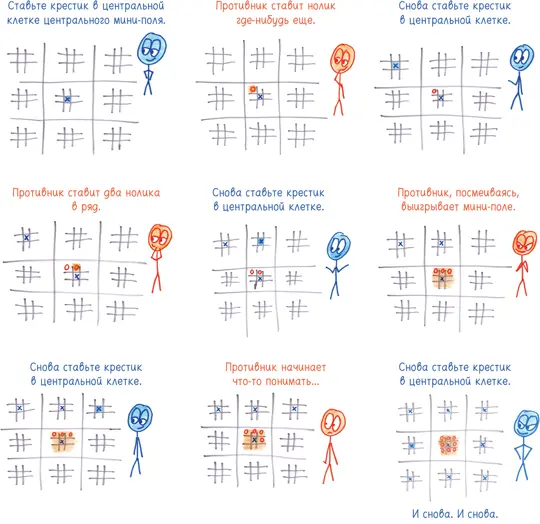
Иными словами, крестики жертвуют центральным мини-полем ради выигрышной позиции на оставшихся восьми. Я полагал, что эта стратегия весьма крута, пока читатели не указали мне на ее глубочайшую глупость. Гамбит Орлина дает небольшое преимущество, но его легко расширить до гарантированно беспроигрышной стратегии [6] Эта стратегия слишком сложна, чтобы полностью изложить ее здесь, но она реализована коллегами из Академии Хана: https://www.khanacademy.org/computer-programming/tic-tac-toe/5946909186326528 . . Вы можете пожертвовать не одним мини-полем, а двумя, завоевав при этом по два крестика на одной прямой на оставшихся семи мини-полях.

Я был смущен и переформулировал старое правило — легкая перенастройка, которая вдохнула в жесткие крестики-нолики новую жизнь.

Новое правило — новая игра.

Именно так развивается математика. Мы выбираем правила и начинаем играть. Когда игра нам приедается, мы меняем правила. Мы вводим новые ограничения и смягчаем старые. Каждое нововведение влечет за собой новые головоломки и вызовы.

По большей части математики не бьются над чужими загадками, а изобретают свои собственные, исследуя, какие ограничения приводят к интересным играм, а какие — к наводящим скуку. В конце концов постоянная смена правил и перескоки от одной игры к другой становятся похожи на отдельную грандиозную нескончаемую игру.

Математика — это логическая игра по изобретению логических игр.

Вся история математики снова и снова иллюстрирует этот тезис. Логические головоломки изобретают, решают и изобретают снова. Например, что произойдет, если я подправлю знакомое уравнение и заменю двойку на другое число: 3, или 5, или 797?

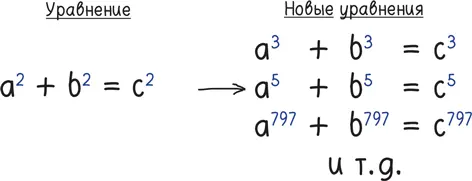
С ума сойти! Я превратил элементарное древнее уравнение, имеющее множество решений в целых числах (например, 3, 4 и 5), в самую досадную задачу, с которой когда-либо сталкивалось человечество, — в великую теорему Ферма. Она тревожила умы математиков около 350 лет, но в 1990-е годы гениальный британец {2} 2 Эндрю Уайлс (род. 1953), профессор Принстонского университета. — Прим. пер. заперся на чердаке и вышел примерно десять лет спустя, щурясь на солнечный свет, с доказательством, что уравнение не имеет целочисленных решений, если степени неизвестных больше двух [7] Я рекомендую прочесть эту историю целиком: Simon Singh, Fermat’s Last Theorem (London: Fourth Estate Limited, 1997). [ Сингх C. Великая теорема Ферма. — М.: МЦНМО, 2000.] .