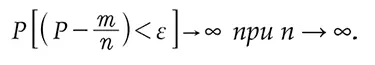Виктор Лёвин - Вероятность как форма научного мышления

Вместе с тем учет гносеологической природы понятий детерминизма и причинности, т. е. их связи с познавательными задачами определенного рода, позволяет характеризовать однозначную причинность как способ выделения упрощенной формы детерминации, связанной с чрезвычайно сильными идеализациями, образцы которых демонстрируют классическая физика, классическая механика, термодинамика и т. д.

Новый тип познавательных задач, выдвигающийся в настоящее время на передний план как имеющий дело с богатым уровнем сложности, прямо связан с отказом от ряда допущений названной формы детерминации (учет всех существенных причин, неограниченная точность фиксации условий и др.) и в силу этого выходит за ее пределы.

Для этого случая решающее значение приобрело истолкование детерминизма с позиций единства определенности и неопределенности. Такого рода единство находит свое выражение, например, в категории «возможность», органически входящей в рамки обобщенной концепции детерминизма. На базе этой категории признается связь, скажем, результатов с воздействиями, однако она приобретает характер некоторой возможностной области. Причем важно, что границы этой сферы возможности имеют достаточно четкие и определенные контуры. Например, при задании ряда граничных условий, обеспечивающих нормальный выстрел из артиллерийского орудия, более или менее четко определяется сектор обстрела в соответствии с законами механики. Вообще же конкретизация общей необходимости налагает границы на область возможностей.

Автор полагает, что сохранение детерминизма в описании сложных ситуаций потребовал выработки средств учета неопределенности и неоднозначности одного уровня сложности системы по отношении к другому. Формализованный подход к решению данной задачи связан с реализацией идеи функции множеств. К числу таковых относится вероятность, истолковываемая в математическом плане как функция, которой становится в соответствии некоторая мера пересечения двух множеств, ограниченная значениями 0 и 1. [42] Колмогоров А. Н. Основные понятия теории вероятностей. М., 1936.

С качественной стороны подобный подход к анализу и описанию сложной детерминации может быть охарактеризован как отказ от поэлементного рассмотрения совокупности детерминирующих факторов, что составляет центральное содержание современного системного подхода.

Хотя надо добавить, что отказ от поэлементного анализа в рамках системного подхода не является абсолютным (и это подчеркивается уже в определении понятия «система»). Напротив, так или иначе, учитываются особенности элементов, но на более глубоком и абстрактном уровне, чем при традиционном рассмотрении (например, посредством фиксации их разнообразия). Важно также, что в рамках системных характеристик осуществляется учет, как внутреннего разнообразия системы, так и внешнего разнообразия воздействий. А это служит основанием для применения много-многозначной формы детерминации.

В данном случае складывается иная ситуация, чем в классической области, поскольку в последней неопределенность лежала просто за пределами точности измерения и отвлечение от неточностей не оказывало значимого влияния на характер детерминации (не искажало ее однозначности). В сложных же системах имеют дело с тем случаем, когда от воздействий нельзя отвлечься.

Многими исследователями было показано что выявление некоторой типичной картины ее сложного поведения объектов должно включать в себя учет отклоняющегося результата в любой момент времени. Понятие вероятности и вероятностное описание оказываются как раз тем инструментом, который способен характеризовать такого рода ситуации. Данная способность обусловлена вхождением неопределенности в качестве существенного момента содержания понятия вероятности. В то же время аппарат теории вероятностей включает ряд ограничений для разброса вероятностей, что дает возможность сохранять определенность. Одним из обобщенных выражений подобного рода ограничений служит, например, закон больших чисел:

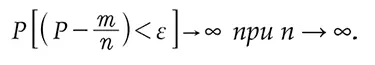
Следует отметить, что для некоторых областей можно, конечно, обойтись без вероятностного описания, хотя в каких-то отношениях оно могло бы оказаться полезным. Возьмем, к примеру, проводник тока. Естественно, что он находится в сети бесконечных взаимодействий, поскольку, вообще говоря, все материальные системы бесконечно сложны. Но, практически, всегда можно создать такие условия, в рамках которых длительное время будут отсутствовать возмущения характера течения тока. Здесь применим тогда однозначный детерминизм. Иной случай представляет, скажем, жизнь биологического индивида. Никак, к примеру, нельзя гарантировать его выживаемость в течение 10 лет. Очевидно, что тогда в самом аппарате описания надо учесть данное обстоятельство. Как следствие – обращение к статистике и вероятности.