Мартин Гарднер - Математические головоломки и развлечения

Аналогичным образом можно показать, что прямоугольник 6x8 будет «прочным» только в том случае, если каждый отрезок сетки границ пересекает ровно два домино. Такой прямоугольник изображен на рис. 250.

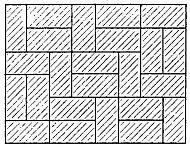
Рис. 250 Прочный прямоугольник 6x8.

В самом общем виде результат можно сформулировать так: из домино можно сложить «прочный» прямоугольник, если его площадь четна, а длина и ширина больше четырех; исключение составляет квадрат 6х6. В действительности, чтобы сложить прямоугольник большего размера, нужно применить к прямоугольникам 5х6 и 6х8 метод увеличения длины или ширины на две единицы.

Проще всего объяснить, как это делается, с помощью рис. 251.

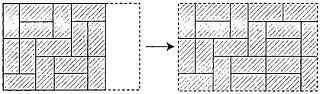
Рис. 251 Общее решение задачи о построении «прочного» прямоугольника.

Для удлинения фигуры в горизонтальном направлении на две единицы надо положить по одному домино рядом с каждым домино, лежащим горизонтально, а все вертикальные домино надо выдвинуть до новых границ, заложив освободившееся место горизонтальными домино.

Может быть, для читателя окажется интересным рассмотреть в качестве кирпичей элементы тримино. В частности, возникает вопрос: каковы наименьшие размеры «прочного» прямоугольника, который можно сложить из двух или большего числа «прямых тримино» (то есть прямоугольников размером 1x3)?

Составил Ю. А. Данилов

Аменицкий Н. Н. Любопытные путешествия. — сер. «Научно-забавная библиотека для семьи и школы», вып. 2. —М.: 1912.

Аменицкий Н. Н. Игра «Nim». — сер. «Научно-забавная библиотека для семьи и школы», вып. 6. — М.: 1912.

Аменицкий Н. Н. Игра «15» (Taquin), «Солитер» (играв «пустынника»): сер. «Научно-забавная библиотека для семьи и школы», вып. 7.— М.: 1912.

Аменицкий Н. Н. Ход коня: сер. «Научно-забавная библиотека для семьи и школы», вып. 8. — М.: 1912.

Аменицкий Н. Н. Арифметические развлечения: сер. «Научно-забавная библиотека для семьи и школы», вып. 17. — М.: 1912.

Аменицкий Н. Н., В. А. Г. Магические квадраты: Арифметические курьезы: сер. «Научно-забавная библиотека для семьи и школы», вып. 5. —М.: 1912.

Аменицкий Н. Н., Сахаров И. П. Забавная арифметика: Хрестоматия для развития сообразительности детей в семье и школе, 4-е изд., доп. /вып. 1. Младший возраст; вып. 2. Средний возраст; вып. 3. Старший возраст. — М.: Товарищество И. Д. Сытина, 1912.

Аменицкий Н. Н., Шиман Е. М., Шукайло К. П. Морские узлы и фокусы с веревками: Что можно сделать из листа бумаги: сер. «Научно-забавная библиотека для семьи и школы», вып. 3. — М.: 1912.

Аменицкий Н. Н., Шиман Е. М., Шукайло К. П. Что можно сделать из листа бумаги (продолжение): сер. «Научно-забавная библиотека для семьи и школы», вып. 4. — М.: 1912.

Анаксиотис. Теорема Фермата. — Киев: 1911.

Арене В. Математические игры и развлечения. — М. —Л.: изд. «Петроград», 1924.

Арифметические игры: сер. «Научно-забавная библиотека для семьи и школы», вып. 1. — М.: 1912.

Архангельский А. Г., Озорной М. Занимательный досуг: Фокусы.

Загадки. Игры со спичками. Шарады. Ребусы. Головоломки. Задачи. Игры. — М.: «Крестьянская газета», 1927.

Баше К. Г. Игры и задачи, основанные на математике. — Спб. — М.: 1877.

Белополъский И. Р. Фокусы и головоломки. — Л.: Гизместпром НКМП РСФСР, 1939.

Бобров СП. Архимедово лето, или История содружества юных математиков. — М.: Детгиз, 1959 (кн. 1), 1962 (кн. 2).

Бобров С.П. Волшебный двурог, или Правдивая история небывалых приключений нашего отважного друга Ильи Александровича Камова в неведомой стране, где правят: Догадка, Усидчивость, Находчивость, Терпение, Остроумие и Трудолюбие и которая в то же время есть пресветлое царство веселого, но совершенно таинственного существа, чье имя очень похоже на название этой удивительной книжки, которую надлежит читать не торопясь: Книга для юных читателей, которые любят точные науки и математику: изд. 2-е, перераб. и доп. — М.: Детская литература, 1967.

Болховитинов В. Н., Колтовой Б. И., Лаговский И. К. Твое свободное время. — М.: Детская литература, 1970.

Буттер И. Занимательные и увеселительные задачи и загадки, изданные Иваном Буттером /изд. 2-е с переменами. — М.: 1844.

Вебер А. Ф. Хитрые загадки — нехитрые отгадки: В мире чисел. — Пг. —М.: Мысль, 1924.