Мартин Гарднер - Математические головоломки и развлечения

9. Термит не может прогрызть 26 наружных кубов и закончить свое путешествие в центральном кубике. Это легко доказать, если представить, что кубики окрашены в шахматном порядке в какие-нибудь два цвета (они расположены, как ячейки в трехмерной шахматной доске или атомы хлора и натрия в кубической кристаллической решетке поваренной соли). Большой куб будет состоять из 13 кубиков одного и 14 кубиков другого цвета. Цвета кубиков на пути термита должны правильно чередоваться. Когда термит прогрызет все 27 кубиков, то начало и конец проделанного им хода должны принадлежать двум из 14 кубиков. Центральный же кубик принадлежит другому набору — из 13 кубиков. Следовательно, решения задачи не существует.

Задача допускает обобщение. Куб четного порядка (то есть склеенный из четного числа кубиков) состоит из одинакового числа кубиков каждого из двух цветов. Центрального кубика нет. Путь термита может начинаться с любого кубика одного цвета и заканчиваться в любом кубике другого цвета. У куба нечетного порядка маленьких кубиков одного цвета на один больше, чем кубиков другого, поэтому путь термита должен начинаться и заканчиваться на кубиках из большего набора. В кубах нечетного порядка 3, 7, 11, 15, 19… центральные кубики принадлежат меньшему набору, и проделанный термитом ход не может заканчиваться в них. У кубов нечетного порядка 1, 5, 9,13,17… центральные кубики принадлежат к большему набору, и в этих случаях ничто не мешает термиту закончить свой путь в самом центре большого куба, разумеется, при условии, что путь начинался в одном из кубиков того же цвета, что и центральный. В кубах нечетного порядка замкнутых ходов быть не может, потому что в них кубиков одного цвета на один больше, чем кубиков другого.

Многие двумерные головоломки также можно решать с помощью аналогичных «проверок на четность». Например, так можно доказать, что ладья не может перейти из одного угла шахматной доски в противоположный угол (по диагонали), побывав по одному разу на всех 64 клетках.

В главе 12 уже говорилось о полимино и его создателе С. Голомбе. После опубликования статьи о полимино на страницах журнала Scientific American A957) игра стала необыкновенно популярным математическим развлечением. Обнаружились сотни новых задач и причудливых конфигураций полимино. О них и пойдет здесь речь.

Напомним, что фигуры, которыми на шахматной доске можно покрыть пять соседних клеток, образующих связную область, носят название пентамино. Существует двенадцать таких фигур. Если эти фигуры расположить так, как показано на рис. 234, то становится видно, что каждая фигура по форме напоминает какую-нибудь латинскую букву, поэтому для запоминания формы и названия фигур (каждую фигуру мы будем называть какой-нибудь буквой) достаточно знать конец латинского алфавита (Т, U, V, W, X, Y, Z) и слово FiLiPiNo.

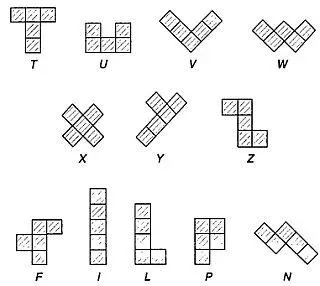
Рис. 234

В главе 12 (см. рис. 71) было показано, что из двенадцати элементов пентамино общей площадью в 60 квадратиков можно сложить прямоугольники четырех размеров: 3х20, 4х15, 5х12 и 6х10. Те же 12 фигур можно уложить на шахматной доске размером 8x8, причем квадрат из четырех лишних клеток (площадь доски равна 64 квадратикам) может находиться в любом месте доски.

Любой элемент пентамино можно утроить с помощью каких-нибудь девяти фигур из числа оставшихся (подразумевается, что из этих девяти пентамино будет сложена фигура, подобная выбранной, но в три раза выше и длиннее). Из двенадцати пентамино можно еще построить два прямоугольника 5x6. Последняя задача носит название задачи на суперпозицию, потому что построенные фигуры можно наложить друг на друга. Голомб сообщил мне пять новых задач на суперпозицию, которые впервые публикуются в этой книге. Если читатель до сих пор не понял всей прелести пентамино, ему необходимо вырезать из картона набор элементов пентамино и поломать голову над некоторыми из приведенных ниже задач.

Во всех головоломках элементы пентамино можно класть на плоскость любой стороной.

1. Разбейте двенадцать пентамино на три группы по четыре элемента в каждой. Затем найдите фигуру площадью в 20 квадратиков, которую можно сложить из элементов каждой группы. Одно из возможных решений изображено на рис. 235.

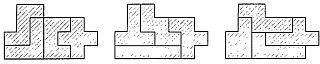
Рис. 235