Георгий Гамов: Занимательная математика

Сэм-младший покачал головой.

— Не сердись, но я не возьму твоих денег. Дело в том, что игра, которую я тебе предлагаю, мошенническая: я могу выбрать такую стратегию замены монет фальшивыми, что при достаточно длинной серии бросаний ты можешь лишь надеяться свести проигрыш до минимума. Но ты непременно проиграешь, а я выиграю. Более того, я могу математически вычислить, какую долю бросаний у меня составит выпадение орла независимо от того, выпадает у тебя орел или решка. И из вычислений я могу узнать, сколько смогу выиграть при достаточно длинной серии бросаний.

Я покажу тебе, как производятся такие вычисления, хотя ты можешь поверить мне на слово. Просто мне кажется, что тебе будет интересно. Вот как это делается.

Напомню, что я хочу вычислить долю бросаний, в которых у меня должен был бы выпасть орел. Обозначим ее через х, а размеры моего платежа через Р.

Рассмотрим сначала, что происходит, когда у тебя выпадают орлы. Всякий раз, когда моя монета падает вверх орлом и у тебя выпал орел, я теряю 9 центов. Так как доля орлов составляет хот общего числа бросаний, это означает, что в моей платежной функции есть член — 9х. Аналогичным образом, всякий раз, когда у меня выпадают решки, а у тебя орлы, я выигрываю 5 центов. Так как решки составляют (1 — х)часть от всех бросаний, в моей платежной функции должен быть член 5(1 — х).

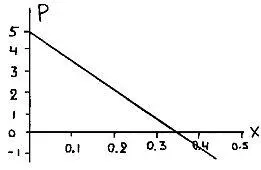
Таким образом, если я запишу мою полную платежную функцию для тех случаев, когда у тебя выпадают орлы, то она окажется

Р орлы= -9x + 5(1 — х),

или просто

Р орлы= -14x + 5.

Вот ее график:

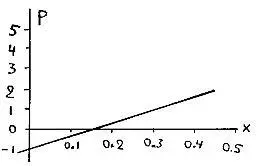
Рассмотрим теперь, что происходит, когда у тебя выпадают peшки. Действуя так же, как прежде, я получаю платежную функцию

Р решки= +5х — 1(1 — х),

Р решки= 6x — 1.

Накладывая оба графика один на другой, мы находим, что они пересекаются при х= 0.3 и Р= 0,8.

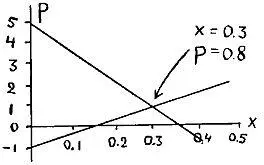
Это означает, что если я заменю 3/10 моих монет на фальшивые и случайным образом распределю фальшивые монеты среди моих монет, то в достаточно длинной серии бросаний я буду в среднем выигрывать 0.6 цента всякий раз, когда твоя и моя монеты выпадут обе либо вверх орлами, либо вверх решками.

— Придумано хитро, хотя, должен признаться, я никак не возьму в толк, как же все получается, — признался Сэм-старший. — Сегодня вечером я собираюсь заглянуть в клуб. Кстати, нет ли у тебя подходящей математической задачки с неожиданным решением? Мне бы хотелось немного позабавиться и позабавить членов клуба.

— Как не быть! — улыбнулся Сэм-младший. Но сначала скажи мне, пожалуйста, сколько членов клуба соберется сегодня вечером.

— Человек эдак тридцать, — прикинул Сэм-старший.

Великолепно! Дело в том, что я хочу рассказать тебе об одной задаче о днях рождения, а для нее людей должно быть достаточно много. Представь себе, что тебе известны дни рождения всех членов клуба, которые соберутся сегодня, какова по-твоему вероятность совпадения дней рождения двух членов клуба? Под днем рождения я имею в виду не год, а только месяц и день.

— Мне кажется, что вероятность совпадения дней рождения у двух из тридцати случайным образом собравшихся людей должна быть что-нибудь около 0,05, но я готов держать пари из расчета 5 к 1.

— Охотно принимаю пари, — согласился Сэм-младший, — а заодно предлагаю тебе заключить пари с кем-нибудь из членов клуба.

Даже если кто-нибудь из них предложит тебе пари из расчета 1 к 1, то рекомендую тебе принять такое пари.

— А вот этого я решительно не понимаю! — воскликнул Сэм-старший.

Между тем перед тобой один из примеров того, что мы называем «мультипликативной природой независимых вероятностей». Ты опрашиваешь членов клуба об их днях рождения до тех пор. пока чей-нибудь день рождения не повторится, и в худшем случае тебе придется опросить всех тридцать членов клуба. Так как опрос продолжается только в том случае, если день рождения очередного члена клуба не совпадает с днем рождения ни одного из ранее опрошенных членов клуба, вероятности, которые требуется перемножить, это вероятности несовпадения дня рождения каждого из вновь опрошенных. А вероятность совпадения дней рождения, разумеется, равна единице минус полученная вероятность несовпадения дней рождения.