Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Как много существует энергетических уровней? Когда ядро переходит с уровня a на уровень b ? Насколько энергетические уровни отстоят друг от друга и почему именно настолько? Подобная постановка вопроса по сути вводит задачу об исследовании атомного ядра в контекст более широкого круга задач — задач о динамических системах, т.е. о наборах частиц, каждая из которых во всякий момент времени занимает определенное положение в пространстве и имеет определенную скорость. По мере развития исследований в 1950-х годах стало ясно, что некоторые из наиболее интересных динамических систем, включая тяжелые ядра, слишком сложны и не поддаются точному математическому анализу в квантовой области. Число энергетических уровней оказалось слишком большим, а возможные конфигурации слишком многочисленны. Такая картина представляет собой самый устрашающий вариант «задачи многих тел» из классической (т.е. доквантовой) механики, где несколько объектов (например, планеты Солнечной системы) действуют друг на друга посредством гравитации.

Когда приходится иметь дело с таким уровнем сложности, точная математика сталкивается с целым рядом проблем, и поэтому исследования в этой области стали опираться на статистику. Если мы не можем определить, что произойдет точно, то, возможно, нам удастся выяснить, что скорее всего произойдет в среднем. Подобные статистические подходы широко развивались в классической механике начиная примерно с 1850 года, т.е. задолго до появления квантовой теории. В квантовом мире все устроено слегка по-другому, но там, по крайней мере, можно использовать значительный объем результатов, накопленных в классической теории. В конце 1950-х и начале 1960-х годов был создан основной аппарат и были разработаны статистические средства для анализа сложных квантовых динамических систем, подобных ядрам тяжелых элементов. Главными действующими лицами здесь были ядерные физики Юджин Вигнер и Фримен Дайсон. Главным же понятием оказались случайные матрицы.

Случайная матрица — это именно то, что следует из ее названия: матрица, составленная из чисел, выбранных случайным образом. На самом деле не совсем случайным. Позвольте привести пример. Вот случайная (4×4)-матрица достаточно специального типа, важность которого я объясню чуть позже. Для экономии места будем все округлять до четырех знаков после запятой:

Первое, что можно заметить по поводу этой хитроумной штуковины, — данная матрица является эрмитовой: она обладает той самой как бы симметрией относительно главной диагонали, которая упоминалась в главе 17.v. Вспомним еще несколько фактов из той главы.

• С каждой (N×N)- матрицей связан многочлен степени N , называемый характеристическим многочленом.

• Нули характеристического многочлена называются собственными значениями матрицы.

• Сумма собственных значений называется следом матрицы (и равна сумме элементов, занимающих главную диагональ).

• В частном случае эрмитовых матриц все собственные значения вещественны и, следовательно, вещественны и коэффициенты характеристического многочлена, а также след.

Для матрицы из приведенного примера характеристический многочлен имеет вид

а собственные значения равны −3,8729, 0,0826, 1,5675 и 4,0864. След равен 1,8636.

Посмотрим теперь повнимательнее на те числа, из которых состоит приведенная выше матрица. Числа, которые мы видим, — вещественные числа на главной диагонали и также вещественные и мнимые части комплексных чисел, занимающих места недиагональных элементов, — случайны в некотором специальном смысле (диагональные случайны с небольшим уточнением, которое будет объяснено ниже). Они выбраны случайным образом из нормального гауссова распределения — знаменитой «колоколообразной кривой», которая повсеместно возникает в статистике.

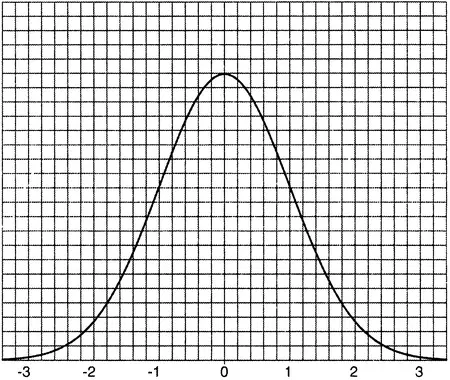
Рисунок 18.1.Нормальное гауссово распределение.

Представим себе стандартную колоколообразную кривую, нарисованную на разлинованном листе бумаги с очень мелкими делениями, так что под кривой расположены сотни квадратиков, образованных разметкой листа (рис. 18.1). Случайным образом выберем один из этих квадратиков; расстояние по горизонтали от него до вертикальной линии, проходящей через середину пика, представляет собой случайное число с нормальным гауссовым распределением. Вблизи самого пика скопилось намного больше этих квадратиков, чем под хвостами кривой, так что с гораздо более высокой вероятностью мы выберем число между +1 и −1, нежели число справа от +2 или слева от −2. Это же видно и из приведенной выше матрицы. (Впрочем, по некоторым техническим причинам элементы на ее главной диагонали в действительности представляют собой случайные гауссовские числа, умноженные на √2, а потому их значения — несколько большие, чем того следовало ожидать.)