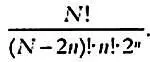Жуан Гомес - Мир математики. т.2. Математики, шпионы и хакеры. Кодирование и криптография

* * *

На рисунке на следующей странице представлена упрощенная схема механизма «Энигмы», где для шифрования используются роторы с алфавитом из трех букв.

В результате каждый ротор имеет только три возможных позиции, а не 26, как в реальной машине.

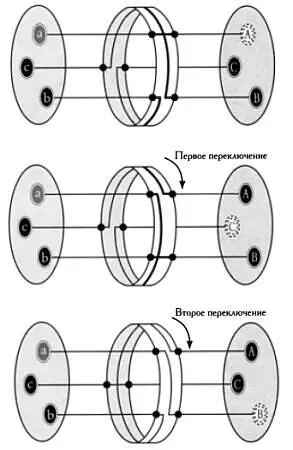
Как мы видим, когда ротор машины «Энигма» находится в исходном положении, каждая буква открытого сообщения заменяется на другую, за исключением буквы А. После шифрования первой буквы ротор поворачивается на одну треть оборота.

В новой позиции буквам теперь соответствуют другие — не те, что в первом шифре.

Процесс завершается третьей буквой, после чего ротор возвращается в исходное положение и последовательность шифров повторяется.

Роторы стандартной машины «Энигма» имеют 26 позиций, по одной на каждую букву алфавита. Следовательно, с одним ротором можно применять 26 различных шифров. Таким образом, начальное положение ротора является ключевым.

Для увеличения количества возможных ключей дизайн «Энигмы» предусматривал до трех роторов, механически соединенных друг с другом. Когда первый ротор делал полный оборот, следующий переключался на одно положение, и так далее до полного оборота третьего ротора, что давало в общей сложности 26 х 26 х 26 = 17576 возможных шифров.

Кроме того, дизайн Шербиуса позволял изменять порядок переключателей, еще больше увеличивая количество шифров, как мы увидим ниже.

Трехроторная машина « Энигма» с частично открытым корпусом, позволяющим видеть коммутационную панель (спереди).

Кроме трех роторов «Энигма» также имела коммутационную панель, расположенную между первым ротором и клавиатурой. Коммутационная панель позволяла перекоммутировать соединения между буквами клавиатуры до соединения с ротором и таким образом добавляла значительное количество кодов к шифру. Стандартный дизайн «Энигмы» предусматривал шесть кабелей, которые могли соединять шесть пар букв. На следующем рисунке показана работа коммутационной панели, снова в упрощенной форме для трех букв и трех кабелей.

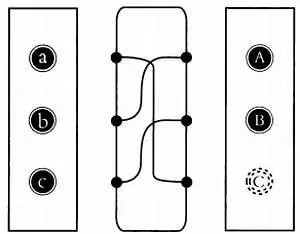
Таким образом, буква Аменяется местами с буквой С, буква В— с буквой А, а С— с буквой В. С добавлением коммутационной панели упрощенная трехбуквенная «Энигма» будет работать следующим образом:

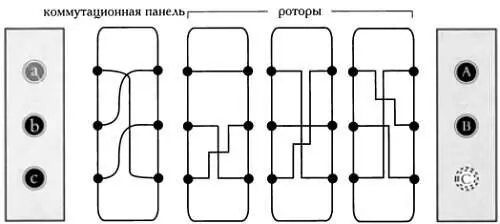
На сколько больше шифров мы получим при, казалось бы, простом добавлении коммутационной панели? Сначала посчитаем количество способов соединения шести пар букв, выбранных из 26 возможных. Число способов выбрать n пар букв из алфавита, содержащего N символов, определяется по формуле:

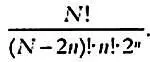
В нашем примере N= 26 и n= 6, что дает нам 100391791500 комбинаций.

Следовательно, общее количество шифров, возможных на машине «Энигма» с тремя роторами из 26 букв и коммутационной панелью с шестью кабелями, считается следующим образом.

1. Количество поворотов трех роторов дает 26 3= 26∙26∙26 = 17 576 комбинаций.

2. Кроме того, три ротора (1, 2, 3) могут меняться друг с другом местами, например, 1–2—3, 1–3—2, 2–1—3, 2–3—1, 3–1—2, 3–2—1. Это дает нам дополнительные шесть комбинаций.

3. Наконец, мы подсчитали число способов соединять пары букв шестью кабелями на коммутационной панели, что дало нам 100391791500 дополнительных шифров.

Общее количество шифров получается умножением перечисленных результатови составляет 6 ∙ 17 576 ∙ 100 391 791 500 = 10 586 916 764 424 000. Таким образом, машина «Энигма» могла шифровать текст, используя более чем десять тысяч триллионов различных шифров. Германское правительство было в полной уверенности, что секретные коммуникации высшего уровня совершенно неуязвимы. И это было большой ошибкой.

Расшифровка кода «Энигмы»

Любой ключ кода «Энигмы» сначала указывал конфигурацию коммутационной панели, а именно возможные соединения шести пар букв, например, B/Z, F/Y, R/C, Т/Н, Е/О и L/J, что означало, что первый кабель менял местами буквы В и Z, итак далее. Во-вторых, ключ определял порядок роторов (например, 2–3—1). Наконец, ключ описывал исходную ориентацию роторов (например, буквы R, V, В показывали, какая буква находится в начальном положении, или начальные позиции).