Игнаси Белда - Том 33. Разум, машины и математика. Искусственный интеллект и его задачи

Оптимальной движущей силой для создания подобных моделей является давление отбора. Бактерия всегда «знает», что ей нужно следовать в направлении, где находится больше питательных веществ. Этот «инстинкт» описывается внутренней моделью, указывающей, что если бактерия будет следовать подобной схеме поведения, то с наибольшей вероятностью гарантирует себе пропитание. Бактерии, которые благодаря кодификации структур и иерархий внутренних агентов смогли создать подобные модели, имеют больше шансов оставить потомство и, следовательно, передать ему это отличительное свойство.

Существует два вида внутренних моделей: явные и неявные. В примере с бактерией, следующей инстинктам в поиске питания, мы имеем дело с неявной моделью, так как она не позволяет ни «думать», ни моделировать альтернативные варианты развития событий. Явные модели, свойственные высшим живым организмам, напротив, позволяют оценивать различные гипотетические сценарии и принимать оптимальные решения после анализа альтернативных вариантов. Примером явной модели в сложной адаптивной информационной системе может служить машина для игры в шахматы, способная анализировать сотни тысяч вариантов на каждом ходу.

Логично, что неявная модель создается и адаптируется к среде по законам эволюции, в то время как для явных моделей скорость адаптации намного выше.

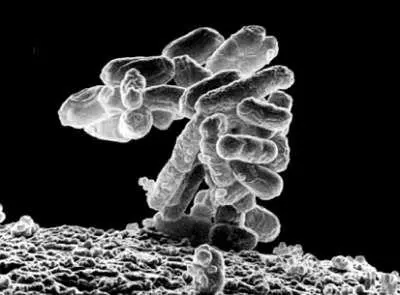
Колония бактерий Escherichia coli, увеличенная в 10 000 раз. Каждая «палочка» обозначает бактерию.

Третий механизм: строительные блоки

Внутренняя модель сложной адаптивной системы, как правило, основывается на ограниченном множестве выборок, описывающих ситуации, произошедшие в прошлом. Эти выборки похожи, но каждая из них обладает определенной новизной. Как сложная адаптивная система может создавать на базе ограниченного предшествующего опыта внутренние модели, полезные в будущем? Ключ к этому парадоксу — использование так называемых строительных блоков, то есть элементов, на которые можно разложить любую систему, среду или сценарий. Рассмотрим в качестве примера финансовую организацию, которая идеально соответствует определению сложной адаптивной системы. Допустим, что организация должна принять решение, выдавать ли клиенту кредит. Главный вопрос заключается в том, сможет ли клиент вернуть кредит в условленный срок. Банк не представляет, сможет ли клиент совершать платежи по кредиту через 15 лет, так как не способен предсказывать будущее. Усложним ситуацию и предположим, что клиент не имеет кредитной истории, то есть банку о нем ничего не известно. В этом случае банк разложит проблему на составляющие и, проанализировав определяющие характеристики нового клиента — уровень его образования, должность, семейное положение и другие, — рассмотрит поведение клиентов со схожим профилем. Эти характеристики будут строительными блоками, описывающими сценарий, с которым столкнулся банк как сложная адаптивная система.

Способность сочетать строительные блоки для создания неявных внутренних моделей развивается по законам эволюции, а обучение явных внутренних моделей обычно проходит в гораздо более короткие сроки, хотя в природе такой способностью обладают только высшие живые организмы.

Классическим примером искусственной жизни (вернее, сложной адаптивной системы) в информатике являются клеточные автоматы. Клеточный автомат — достаточно простое понятие, предназначенное для изучения сложности высших систем.

Оно было предложено авторитетными математиками и друзьями Станиславом Уламом (1909–1984) и Джоном фон Нейманом (1903–1957).

Американский математик польского происхождения Станислав Улам.

Автоматы — это математические модели, которые для определенных входных значений запрограммированы на выполнение ряда инструкций. Иными словами, автомат — это обобщение алгоритма или компьютерной программы. Таким образом, в информатике автоматами является все, от программируемого микрочипа, способного выполнять определенные действия, и заканчивая операционной системой. Еще один пример автомата, о котором мы уже рассказывали, это машина Тьюринга.

Как правило, теоретические автоматы, подобные машине Тьюринга, — это устройства, фиксирующие входные сигналы и печатающие выходные значения на одномерных лентах. Автомат проходит вдоль ленты и считывает написанные на ней символы, как показано на рисунке. На основе считанных символов и заложенных в автомат инструкций он выполняет то или иное действие, к примеру, печатает на определенном участке ленты некий символ.