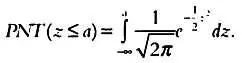Живительная математическая теорема, называемая «центральной предельной теоремой», гласит, что на очень больших генеральных совокупностях (при анализе множества деталей, изготовленных на станке, множества избирателей в стране, роста, веса, психологических характеристик людей, поведения групп людей и т. д.) рассматриваемые значения стремятся к нормальному распределению, следовательно, средние значения на выборках, взятых из этой совокупности, также подчиняются нормальному закону и совпадают со средними по всей совокупности. Среднеквадратическое отклонение на выборках также подчиняется нормальному закону и равняется среднеквадратическому отклонению генеральной совокупности.
Центральная предельная теорема является основным связующим звеном между значениями на выборке (несколько объектов) и значениями на большой генеральной совокупности (множество объектов) и показывает, насколько большое значение имеет нормальное распределение вероятности в статистических исследованиях.
По данным периодически проводимых опросов активного населения можно определить параметры всего населения страны с определенной погрешностью, которая описывается доверительным интервалом, о чем мы уже говорили выше.
Вероятность P(z)возникновения события zвычисляется как площадь, ограниченная графиком функции распределения и осью ОХ. Поэтому нет смысла говорить о Р(0,45), так как, во-первых, в связи с погрешностями измерения, неизбежными для любого инструмента, можно говорить лишь об определенном интервале, во-вторых, потому что площадь полученной области будет равна 0.
* * *
СТАНДАРТИЗОВАННОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Стандартизованное нормальное распределение — это упрощенное нормальное распределение изучаемого параметра или переменной. Все значения х iизучаемой переменной меняются: из них вычитается среднее значение i, после чего результат делится на среднеквадратическое отклонение σ. Стандартизованная переменная обозначается буквой z.
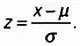
Таким образом, центральным значением множества х i становится не μ , а 0. При делении на σраспределение становится стандартизованным, среднеквадратическое отклонение принимает значение σ = 1. Таким образом, одно и то же распределение (один и тот же график, одну и ту же функцию и одну и ту же таблицу значений) можно использовать для любого нормального распределения после замены переменной, а благодаря этой замене при анализе любого нормального распределения можно использовать одну и ту же таблицу значений.
При переходе к новой переменной (от х к z) все распределения статистических переменных, подчиняющихся нормальному закону, определяются одной и той же функцией распределения (так 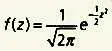 при среднем значении, равном 0, и среднеквадратическом отклонении, равном 1.
при среднем значении, равном 0, и среднеквадратическом отклонении, равном 1.
* * *
При изучении непрерывных статистических переменных имеет смысл говорить только о вероятности попадания значения z на определенный интервал 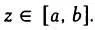 .
.
Тогда площадь, ограниченная графиком, есть интеграл от функции плотности:
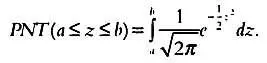
Также можно говорить о вероятности того, что величина z будет не больше определенного значения, то есть будет принадлежать открытому интервалу [ 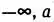 ]. Эта вероятность рассчитывается так:
]. Эта вероятность рассчитывается так:
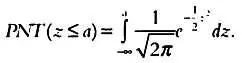
В обоих случаях интеграл позволяет найти необходимую площадь.
Графически вероятность того, что значение zбудет меньше или равно а, изображается областью, выделенной серым цветом на следующем графике, и вычисляется с помощью интеграла:
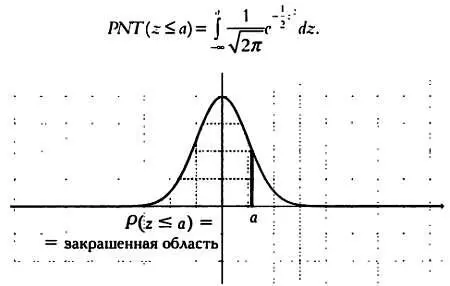
Значение этого интеграла можно вычислить только с помощью методов аппроксимации. С их применением были составлены таблицы распределения вероятностей для стандартизованного нормального закона распределения, позволяющие выполнить любое статистическое исследование, в котором фигурирует нормальное распределение. Эти таблицы можно найти в любой книге по основам статистики, и они позволяют вычислить следующие вероятности:
Читать дальше

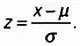
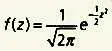 при среднем значении, равном 0, и среднеквадратическом отклонении, равном 1.
при среднем значении, равном 0, и среднеквадратическом отклонении, равном 1.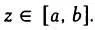 .
.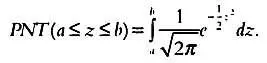
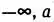 ]. Эта вероятность рассчитывается так:
]. Эта вероятность рассчитывается так: