Банеш Хофман - Альберт Эйнштейн. ТВОРЕЦ И БУНТАРЬ.

Можно было бы ожидать, что, с учетом своего движения относительно А, В измерит скорость своих световых импульсов, движущихся относительно его корабля влево, и она окажется равной с + 17 000, а скорость движущихся вправо импульсов — куда меньшей, а именно, с — 17 000.

Но если бы это было так, то нарушился бы первый постулат Эйнштейна. Как же так? Ведь если А и В проводят в точности одни и те же эксперименты на борту своих кораблей и совершают равномерное движение, то они должны получить одинаковые результаты. Таким образом, В, как и А, измерив обе скорости, обнаружит, что они равны с. В самом деле, независимо от того, как быстро движется В относительно А, пытаясь догнать удаляющийся импульс света, свет всегда будет удаляться от него с одной и той же скоростью с. В не может догнать удаляющийся свет точно так же, как на Земле невозможно достичь горизонта. Ни одно материальное тело не может двигаться с быстротой света. В этом поразительном выводе неожиданно заключен ответ на вопрос 16-летнего Эйнштейна о движении за световой волной.

Поскольку итог наших рассуждений крайне неожидан, попробуем рассмотреть его с другой точки зрения — хотя бы для того, чтобы проверить, следует ли наш вывод из двух принципов Эйнштейна. Предположим, А обнаружил, что скорость в обоих направлениях равна с, в то время как для В она оказалась равной с + 17 000 в одном направлении, и с — 17 000 — в другом. Тогда А мог бы с полным правом заключить, что он находится в состоянии абсолютного покоя, а В передвигается с абсолютной скоростью 17 000 км в секунду. Однако этот вывод противоречил бы принципу относительности.

Человек менее гениальный, столкнувшись с подобным крайне неприятным следствием двух, казалось бы, безобидных постулатов, немедленно отказался бы от какого-нибудь из них. Но Эйнштейн смело сохранил оба постулата, ведь они были ему нужны именно потому, что выражали самую суть проблемы. Само правдоподобие каждого из них, взятого в отдельности, обеспечивало его теории прочный фундамент. В столь сложной, полной неожиданностей области физики Эйнштейн не мог позволить себе возводить здание своей теории на зыбучем песке.

Теперь нам понятно, что Эйнштейн имел в виду под словом «противоречие». И все-таки это противоречие он определил как «лишь кажущееся», подразумевая под этим, что собирается каким-то образом его разрешить. Но как именно?

Мы подошли к критическому моменту в наших рассуждениях. Совершенно очевидно, что для выхода из создавшегося положения требовались какие-то радикальные средства. Идея, которая осенила Эйнштейна в то знаменательное утро, состояла в необходимости отказа от привычного, заботливо взлелеянного многими поколениями представления о времени.

Чтобы понять революционную идею Эйнштейна о времени, вернемся к нашим кораблям А и В и дадим их капитанам новое задание. Предположим, что на борту этих кораблей установлено по две пары точнейших часов а 1, а 2, b 1 и b 2 так, как это изображено на рисунке. Для удобства условимся, что длина кораблей составляет миллионы км — тогда мы сможем говорить о минутах, а не о миллиардных долях секунды.

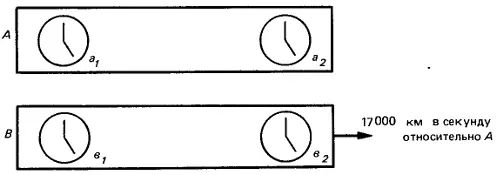
А посылает импульс света от а 1к а 2, откуда свет немедленно отражается назад к а 1. Свет покидает а 1 , когда стрелки часов а 1 показывают полдень, и достигает а 2 , когда стрелки а 2 показывают 3 минуты первого. Из этого мы не можем с уверенностью заключить, что свету понадобилось 3 минуты, чтобы пройти путь от а 1 до а 2 : а вдруг, к примеру, работник, устанавливавший часы, нечаянно передвинул стрелки? Как же сделать так, чтобы часы а 2 шли синхронно с часами а 1? Давайте рассмотрим этот дважды пройденный путь. Предположим, что свет покидает а 1, когда стрелки этих часов показывают полдень, достигает а 2, когда а 2 показывают 3 минуты первого, и возвращается к а 1, когда на а 1— 4 минуты первого. Мы немедленно заподозрили бы что-то неладное. Часы утверждают, что свету понадобилось 3 минуты, чтобы пройти расстояние от а 1 до а 2 , и всего 1 минута на обратный путь от а 2 к а 1. Тогда мы поступим самым простым и очевидным образом: передвинем минутную стрелку а 2 на одно деление назад. Проведем эксперимент вновь — часы покажут, что свету понадобится 2 минуты на путь от а 1 до а 2 и 2 минуты на обратный путь от а 2 до а 1 . Поскольку мы уже убедились, что нам и на пути туда, и на пути обратно нужна одна и та же скорость света с, мы согласились бы с Эйнштейном, что ход часов а 1 и а 2 синхронизирован. И если чуть позднее что-либо приключится в а 1 , когда стрелки а 1 будут показывать 4:30, а еще что-нибудь произойдет в а 2, когда на а 2 будет также 4:30, мы согласимся с Эйнштейном, что эти два не связанных между собой события произошли одновременно.