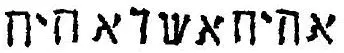Александр Андреев - Время Шамбалы

Великая Универсальная Наука — Религия представляет себе Божество проявляющимся в трех взаимно проникающих, служащих логическим расширением предшествующего мирах.

Эти миры наш ограниченный разум может представить себе так:

1. В нашем представлении всякому формированному и качественному бытию необходимо предшествует абсолютная бесконечная субстанция. Она без качества. Она не ограничена. О ней можно лишь сказать, что она есть.

В Исходе III 13–15: Божество называет себя:

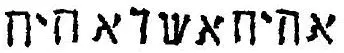
«Ehie asher ehie» (др. евр.) — Я сущий, который пребудет (букв.: «Буду, который буду»).

Греческие переводчики LXX перевели это: ('εγω ειμι o'Ω) [282].

Титул высшего Божества солнечного культа Египта: Nuc-pu-nuc.

По-латыни этому соответствует: ego sum ego [283].

Утверждением, что эта абсолютная бескачественная субстанция Есть, мы допускаем в ней лишь скрытую, ускользающую от нашего восприятия возможность перейти в реальность. До тех пор она лишь полна потенциальности.

2. Возникшее из нее как логическое ее содержание, бывшее в ней потенциально включенным формирующее начало определяет и ограничивает ее в реально существующее, подлежащее уже нашему представлению.

3. Это первое реальное, очевидно, есть общая форма, логически включающая в себя все дальнейшие многообразные формы, ибо позади нее, за ней и над ней, т. е. прежде нее, лишь бесформенная, неограниченная, неопределенная сущность. Эта общая форма обнимает всякую частную форму.

Пример из области естествознания:

Неорганическая форма — химизм заключается в растительной протоплазме. Растительная форма — клетка-протоплазма заключается в животной. Другими словами: химизм проницает и растительную, и животную формы.

3. Из совокупности всеобъемлющей, всесодержащей потенциальной субстанции и всеобъемлющей общей формы, первого формирующего начала в ней потенциально содержащегося, из нее восставшего, оформляется впервые реальный универсальный механизм мироздания с его бесконечно разнообразными применениями. Результат применения его — бесконечное число определенных и ограниченных созданий.

4. Как наиболее близко к действительности представить себе абсолютную бескачественную, неограниченную и в то же время все наполняющую первосущность?

5. Вообразим себе математическую точку.

Как известно, она не имеет измерений. У нее нет протяженности, толщины, длины, ширины, высоты.

Она не занимает пространства.

Наиболее близкое к ней графическое изображение, доступное нашим несовершенным приборам, — это мельчайший укол, занимающий как можно меньше пространства.

6. Представим теперь эту точку постоянно развивающейся и распространяющейся во все стороны — как бы распухающей. Этот процесс представляется нам как бесконечно распухающий шар.

Пространство безгранично.

Шар бесконечно распухает.

Представим себе, что на пути распухания он обнял и поглотил нас, нашу планету, солнечную систему, звезды, миры — конца его распуханию нет. В своем развитии точка выполняет и обнимает все.

В точке, не имеющей измерений, очевидно, скрыты в потенциальности все измерения.

Неограниченное бесконечное недоступно нашему восприятию.

Другими словами, оно для нас нереально.

Чтобы стать реальностью, оно должно быть ограничено.

Единственный способ ограничения этого бесконечного распухания, очевидно, принятие возрастающего из центра — точки радиуса определенного, ограниченного размера.

Тогда мы получим определенного размера шар.

Шар древняя Мудрость устами наследника величайшего из посвященных классического мира Пифагора, устами ученика Платона, называет Совершеннейшим всеобъемлющим телом — это 3 мира (Бриа, Ецира, Асиа).

Бесконечно распухающая, развивающаяся точка передает точно механизм и содержание представления о бесконечности вселенной.

Представление о шаре близко к представлению об истинном объеме вселенной, воспринимаемом нашим разумом.

Будет ли это представление представлением о Первом Осязаемом в прямом смысле?

Нет!

Почему?

Что такое вещество? (Осязаемое надписано сверху. — А. А. )

То, что можно взвесить, измерить точно.

Что мы можем измерить точно?

Лишь прямолинейные протяженности.

Можно ли точно измерить окружность?

Нельзя.

Можно ли точно измерить объем шара?