Манжит Кумар - Квант. Эйнштейн, Бор и великий спор о природе реальности

Для упрощения задачи Бор предположил, что движение электронов вокруг ядра происходит только по круговым орбитам. Зоммерфельд посчитал, что это ограничение можно снять. Он разрешил электронам, как планетам вокруг солнца, двигаться по эллипсоидальным орбитам. Зоммерфельд знал, что с точки зрения математики окружность — это специальный случай эллипса. Поэтому круговые орбиты, по которым двигаются электроны, — это только подмножество всех возможных квантованных эллипсоидальных орбит. Квантовое число п в модели Бора определяет стационарное состояние, разрешенную круговую орбиту электрона, и соответствующий этому состоянию энергетический уровень. Значение п также определяет и радиус данной орбиты. Однако чтобы определить форму эллипса, требуются два числа. Поэтому, чтобы проквантовать эллипсоиды, Зоммерфельд ввел еще одно “орбитальное” квантовое число k. Из всех возможных эллипсоидальных орбит число k отбирает те, которые разрешены при данном значении п.

В модифицированной модели Зоммерфельда главное квантовое число n определяет допустимые значения k 49. Если n = 1, то k = 1; когда n = 2, то возможны значения k = 1 и k = 2; при n = 3 значения k = 1,2,3. Для заданного значения n число k может принимать все целочисленные значения от единицы до n . Все орбиты при k = n являются круговыми. Однако если k меньше n , то орбита — эллипс. Например, когда n = 1 и k = 1, орбита — это окружность, радиус которой r называется боровским радиусом. Если n = 2, а k = 1, то орбита — эллипс. Но если n = 2 и k = 2, то орбита — окружность, радиус которой равен 4 r . Таким образом, если атом водорода находится в квантовом состоянии n = 2, его единственный электрон может находиться на одной из двух орбит, где k = 1 или k = 2. В состоянии с n = 3 электрон может находиться на одной из трех орбит. Эти орбиты суть эллипс при n = 3 и k = 1; эллипс — при n = 3 и k = 2; окружность — при n = 3 и k = 3. В модели Бора при n = 3 только одна разрешенная орбита, а в модифицированной модели Зоммерфельда таких орбит три. Эти дополнительные стационарные состояния позволяют объяснить расщепление линий серии Бальмера.

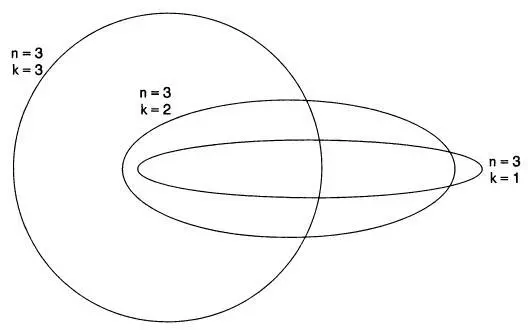
Рис. 8. Электронные орбиты для n = 3 и k = 1,2,3 в модели атома водорода Бора — Зоммерфельда.

Чтобы объяснить расщепление спектральных линий, Зоммерфельд обратился к теории относительности Эйнштейна. Как и скорость кометы, вращающейся вокруг Солнца, скорость электрона на эллиптической орбите возрастает, когда он приближается к ядру. Но, в отличие от кометы, скорость электрона настолько велика, что его движение надо описывать уравнениями теории относительности. Отсюда следует, что увеличивается масса электрона. Релятивистское увеличение массы приводит к очень небольшому изменению энергии. В состоянии n = 2 две орбиты, k = 1 и k = 2, имеют разные энергии, поскольку при k = 1 орбита эллиптическая, а при k = 2 — круговая. Небольшая разница энергий означает наличие двух энергетических уровней и, следовательно, двух спектральных линий там, где теория Бора предсказывает только одну. Однако было еще два явления, которые не удавалось объяснить и с помощью квантового атома Бора — Зоммерфельда.

В 1897 году голландский физик Питер Зееман обнаружил, что в магнитном поле одна спектральная линия расщепляется на несколько линий или компонент. Если магнитное поле выключить, расщепление пропадает. Этот эффект был назван эффектом Зеемана. В 1913 году немецкий физик Иоханнес Штарк обнаружил, что спектральная линия расщепляется и тогда, когда атом помещен в электрическое поле 50. После опубликования статьи Штарка Резерфорд связался с Бором: “Мне кажется, что теперь самое время высказаться об эффекте Зеемана и об аналогичном эффекте в электрическом поле. Их надо, если это возможно, согласовать с Вашей теорией” 51.

Еще до Резерфорда Зоммерфельд обратился к Бору с таким же предложением. Вскоре после публикации первой части своей “трилогии” Бор получил от него письмо с поздравлениями. Зоммерфельд, в частности, спрашивал: “Не собираетесь ли Вы использовать свою модель для объяснения эффекта Зеемана? Я бы очень хотел разобраться в этом” 52. Однако объяснить эффект Зеемана удалось Зоммерфельду, а не Бору. Решение было очень остроумным. До этого он ввел в рассмотрение эллиптические орбиты, по которым движутся электроны. Таким образом, увеличилось число допустимых квантованных орбит, где может находиться электрон при данном энергетическом состоянии атома, например при n = 2. И Бор, и Зоммерфельд считали, что орбиты — неважно, круговые или эллиптические, — лежат в одной плоскости. Пытаясь осмыслить эффект Зеемана, Зоммерфельд понял, что ориентация орбит в пространстве и есть недостающее звено. Электрон в магнитном поле может выбирать из большего числа разрешенных орбит. Эти орбиты по-разному ориентированы относительно магнитного поля. Чтобы проквантовать ориентацию орбит, Зоммерфельд ввел так называемое “магнитное” квантовое число т. Для данного значения главного квантового числа n число m может принимать все целочисленные значения от - n до n 53. Так, если n = 2, то значения m равны -2; -1; 0; 1; 2.