Стивен Вайнберг - Объясняя мир. Истоки современной науки

Более убедительное доказательство закона преломления дал математик Пьер де Ферма (1601–1665). Он сделал его по образцу доказательства правила равенства углов падения и отражения Герона Александрийского, но основывался на предположении о том, что лучи света проходят свой путь за наименьшее время, а не проходят наименьшее расстояние. Как показано в техническом замечании 28, это предположение приводит к правильной формуле, где n – это отношение скорости света в среде А к его скорости в среде В и, таким образом, больше единицы, если А – это воздух, а В – вода или стекло. Декарт никогда не смог бы вывести такую формулу для n , поскольку для него свет двигался мгновенно (как мы увидим в главе 14, другое доказательство с правильным результатом было дано Христианом Гюйгенсом. Оно было основано на теории Гюйгенса о том, что свет – это движущееся волновое возмущение среды, и не нуждается в априорном предположении Ферма о том, что свет проходит свой путь за наименьшее возможное время).

Декарт сделал великолепное дополнение к закону преломления: в своей «Метеорологии» он использовал соотношение между углами падения и преломления, чтобы объяснить появление радуги. Это было величайшее достижение Декарта как ученого. Аристотель доказывал, что цвета радуги получаются, когда свет отражается от капель воды, рассеянных в воздухе {240}. Так же, как мы уже видели в главах 9 и 10, в Средние века и аль-Фариси, и Дитрих из Фрайбурга считали, что радуга получается, когда свет преломляется, проходя через капли воды, взвешенные в воздухе. Но до Декарта никто не представлял детально численного описания того, как это происходит.

Вначале Декарт провел эксперимент, используя стеклянный сосуд сферической формы с тонкими стенками, наполненный водой, в качестве модели капли дождя. Он заметил, что, когда лучи света проходят сквозь шар в разных направлениях, свет, который выходит обратно под углом примерно 42° к углу падения, становится «полностью красным и несравнимо более ярким, чем остальные лучи». Он пришел к заключению, что радуга (или, по крайней мере, ее красный цвет) образует в небе арку, когда угол между направлением на радугу и направлением от нее на солнце равен примерно 42°. Декарт предположил, что лучи света преломляются, попадая в каплю воды, отражаются от ее внутренней поверхности и затем снова преломляются, когда попадают из капли в воздух. Но как объяснить свойство радуги посылать лучи из капель именно под углом в 42° к направлению их падения?

Чтобы ответить на этот вопрос, Декарт предполагает, что лучи света попадают в сферическую каплю по десяти различным параллельным направлениям. Он присвоил каждому из этих лучей то, что сегодня называют прицельным параметром b – величина кратчайшего расстояния до центра капли, на котором луч прошел бы, если бы проходил сквозь каплю прямо, не преломляясь. Первый луч был выбран так, что если бы он не преломлялся, то прошел бы на расстоянии от центра капли, равном 10 % радиуса R капли (то есть b = 0,1 R ). При этом десятый луч был выбран так, чтобы задеть поверхность капли по касательной ( b = R ). Все остальные лучи были равномерно распределены между ними. Декарт описал путь каждого луча, как он преломился, войдя внутрь капли, отразился от ее внутренней поверхности и снова преломился, покидая каплю, используя закон равенства углов отражения Евклида и Герона и свой собственный закон преломления, приняв показатель преломления воды n за 4/3. В таблице приводятся значения, полученные Декартом для угла φ между выходящим из капли лучом и направлением его падения для каждого луча, и результаты моих собственных расчетов, при которых я использовал тот же самый показатель преломления:

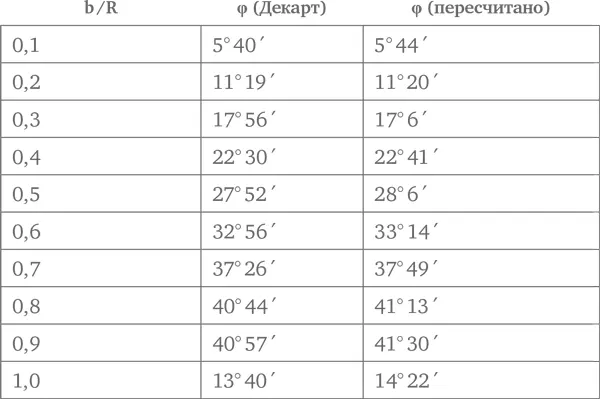
Неточность некоторых результатов Декарта может быть связана с ограниченностью математических средств в то время. Я не знаю, была ли у него возможность пользоваться таблицей синусов, но у него точно не было ничего, хотя бы отдаленно напоминающего современный микрокалькулятор. Тем не менее эти результаты выглядели бы лучше, если бы Декарт округлил их до ближайшего целого градуса, а не до 10 минут угла.

Как заметил Декарт, угол φ близок к 40° для достаточно широкого диапазона прицельных расстояний b . Далее он повторил расчеты для восемнадцати еще более близко расположенных лучей, значения b для которых отличались от 80 до 100 % радиуса капли, при этом угол φ был равен примерно 40°. Декарт выяснил, что для четырнадцати из этих восемнадцати лучей угол φ находился в промежутке от 40° до максимальной величины 41° 30´. Таким образом, эти теоретические расчеты подтвердили его экспериментальные данные, упомянутые ранее, где угол наиболее яркого луча был округленно равен 42°.