Дмитрий Оголихин - Метод конечных элементов

Метод конечных элементов – один из т. н. сеточных методов. Такие методы предполагают рассмотрение цельной конструкции как совокупности отдельных конечных элементов , как показано на рисунке 1.

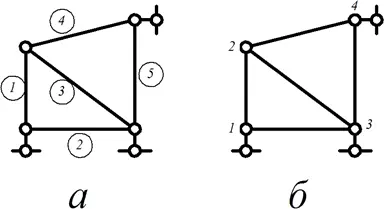
Рисунок 1. Разбиение конструкции на конечные элементы. а – нумерация конечных элементов; б – нумерация узлов.

В качестве конечных элементов выступают знакомые нам из сопротивления материалов и строительной механики стержни, балки, плиты, оболочки и т. п. По сути своей решение методом конечных элементов сводится к решению уравнения задачи в динамической постановке:

M∙d 2u/dt 2+C∙ du/dt+K∙u = P

где M – матрица масс конструкции;

C – матрица демпфирования конструкции;

K – матрица жёсткости конструкции;

d 2u/dt 2 – вектор ускорений узлов конструкции;

du/dt – вектор скоростей узлов конструкции;

u – вектор перемещений узлов конструкции;

P – вектор узловых нагрузок.

Если вектор узловых сил P не меняется во времени, то задача сводится к статической , описываемой уравнением:

K∙u = P

Так как многие задачи в машиностроении сводятся к статическим , то упор в книге будет делаться на них. Для рассмотрения задач будет использоваться среда MathCad 15.

Для того, чтобы решить уравнение необходимо провести предварительную подготовку. В общем и целом, алгоритм решения выглядит следующим образом:

1) Разбиение конструкции на конечные элементы;

2) Составление матрицы жёсткости каждого конечного элемента;

3) Перевод матрицы жёсткости из локальной системы координат в глобальную;

4) Составление глобальной матрицы жёсткости всей конструкции;

5) Приведение нагрузок к узловым;

6) Учёт закреплений;

7) Решение уравнения:

u = K -1∙P

Операция 1, на взгляд автора, интуитивно понятная и не требует пояснений.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.