Митио Каку - Гиперпространство - Научная одиссея через параллельные миры, дыры во времени и десятое измерение

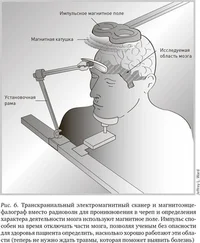
Несмотря на то что в целом картина выглядела убедительно, в 1950–1960-е гг. физиков сбивало с толку то, что поле Янга – Миллса не относится к «перенормируемым», т. е. не дает конечных и значимых величин применительно к простым взаимодействиям. Таким образом, с точки зрения описания слабых и сильных взаимодействий квантовая теория бесполезна. Квантовая физика уперлась в глухую стену.

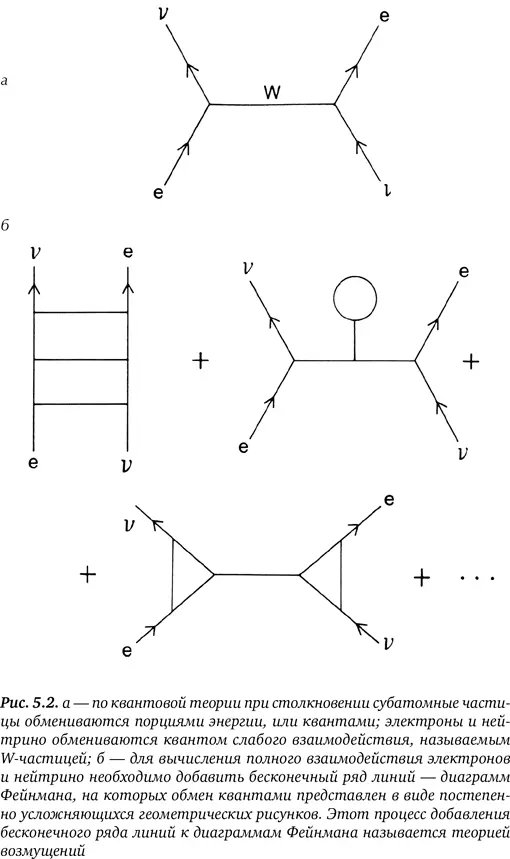
Проблема возникла, так как физики, вычисляя, что произойдет при столкновении двух частиц, пользовались так называемой теорией возмущений, т. е. завуалированным способом указать, что они прибегали к хитроумным приближениям. К примеру, на рис. 5.2, а мы видим, что происходит при столкновении электрона с другой частицей, участвующей в слабом взаимодействии, – неуловимым нейтрино. На первый взгляд, это взаимодействие можно описать диаграммой (она называется « диаграммой Фейнмана »), показывающей, что обмен квантом слабого взаимодействия – W-частицей – происходит между электроном и нейтрино. В первом приближении мы получаем грубое, но приемлемое соответствие экспериментальным данным.

Однако согласно квантовой теории в наше первое приближение следует внести небольшие поправки. Чтобы сделать наши вычисления строгими, надо также добавить к диаграммам Фейнмана все возможные линии, в том числе с «петлями» на них, как на рис. 5.2, б . В идеале эти квантовые поправки должны быть совсем маленькими. Ведь как мы уже упоминали, квантовая теория для того и предназначена, чтобы вносить крохотные квантовые поправки в ньютонову физику. Но, к ужасу ученых, эти квантовые поправки, или «петлевые линии», оказались не маленькими, а бесконечными. Как ни мудрили физики над своими формулами, как ни пытались замаскировать эти бесконечные величины, расхождения упорно обнаруживались при любых вычислениях квантовых поправок.

Более того, поле Янга – Миллса приобрело устрашающую репутацию метода, головоломно усложняющего расчеты – в сравнении с более простым полем Максвелла. Согласно мифам, с которыми ассоциируется поле Янга – Миллса, для практических вычислений оно совершенно не подходит ввиду своей сложности. Вероятно, 'т Хоофту просто повезло: будучи аспирантом, он еще не успел заразиться предубеждениями маститых физиков. Пользуясь методами, которые первым описал его научный руководитель Мартинус Велтман, 'т Хоофт доказал: всякий раз, когда мы сталкиваемся с «нарушением симметрии» (о нем мы поговорим далее), поле Янга – Миллса приобретает массу, но остается конечной теорией. 'т Хоофт продемонстрировал, что благодаря графам с петлями можно не рассматривать бесконечности или нивелировать их влияние.

Почти через 20 лет после того, как поле Янга – Миллса было предложено авторами, Хоофт наконец доказал, что оно является корректной и однозначной теорией взаимодействия частиц. Известие о работе 'т Хоофта распространилось молниеносно. Нобелевский лауреат Шелдон Глэшоу вспоминает, что он, услышав эту новость, воскликнул: «Либо этот парень полный кретин, либо величайший гений, появившийся в физике впервые за много лет!» {45}Дальнейшее развитие событий было стремительным. Быстро выяснилось, что верна более ранняя теория слабого взаимодействия, предложенная в 1967 г. Стивеном Вайнбергом и Абдусом Саламом. К середине 1970-х гг. поле Янга – Миллса было применено к сильному взаимодействию. Тогда же, в 1970-х гг., к физикам пришло ошеломляющее понимание, что поле Янга – Миллса может оказаться ключом к тайнам всей ядерной материи.

Таким оказался недостающий элемент головоломки. Секрет «дерева», связующий воедино материю, – не геометрия Эйнштейна, а поле Янга – Миллса. По-видимому, именно оно, а не геометрия, представляло собой главный урок физики.

Сегодня поле Янга – Миллса открыло возможность всеобъемлющей теории материи. Мы настолько уверены в этой теории, что ласково называем ее Стандартной моделью .

Стандартная модель способна объяснить все экспериментальные данные, касающиеся субатомных частиц с энергией вплоть до 1 ТэВ (энергией, возникающей при ускорении электрона в поле, созданном разностью потенциалов в триллион вольт). Это почти предел для ускорителей, существующих в настоящее время [10]. Следовательно, можно без преувеличения сказать, что Стандартная модель – самая удачная теория в истории науки.