Останавливаясь на этом понятии, нельзя не остановиться на основных множествах чисел, которые активно применяются в счёте и проведении различных операций, но в последующих главах некоторые из этих множеств будут рассмотрены уже более подробно со всеми свойствами.
Первым множеством является множество натуральные числа – это числа, получаемые при естественном счёте, обозначаясь через N. При этом натуральные числа являются замкнутыми относительно сложения и умножения. А сложение и умножение натуральных чисел коммутативно и ассоциативно, также умножение натуральных чисел дистрибутивно относительно сложения и вычитания.
Второй множество – множество целых чисел состоит из чисел получаемые при объединении множества натуральных чисел с множеством чисел противоположных натуральным и нулём, обозначаются как Z. Любое целое число можно представить как разность двух натуральных. Целые числа замкнуты относительно сложения, вычитания и умножения. Также это множество является кольцом.
Третье множество – множество рациональных чисел, обозначаемых через Q, представляют собой числа, представимые в виде дроби m/n , где числитель – целое число, а знаменатель – натуральное. Рациональные числа замкнуты уже относительно всех четырёх арифметических действий: сложения, вычитания, умножения и деления (кроме деления на ноль, эта операция уже принадлежит ингенциальному множеству); такое множестве или точнее алгебраическая структура является полем.
Четвёртое множество – действительные или вещественные числа, обозначаемые через R, это числа, представляющий собой расширение множества рациональных чисел, замкнутое относительно некоторых операций предельного перехода. Множество вещественных чисел обозначаются через R. Его можно рассматривать как пополнение поля рациональных чисел Q при помощи нормы, являющейся обычной абсолютной величиной. Кроме рациональных чисел, это множество также включает в себя множество иррациональных чисел I, не представимых в виде отношения целых.
И наконец, одно из самых известных на сегодня множеств, пятое множество – комплексное множество C, состоящее из чисел, являющиеся расширением множества действительных чисел. Они могут быть представлены через вещественную и комплексные части, с участием мнимой единицы, которая в чётных степенях даёт -1. Комплексные числа подразделяются на алгебраические и трансцендентные. При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число – действительным алгебраическим. Более общими классами чисел, чем алгебраические, являются периоды – числа, выражающие объём в n-мерном пространстве, вычислимые – число выводимое при помощи заданного алгоритма с сколь угодной точностью и арифметические числа – множество натуральных чисел, определяющиеся формулой первой степени.
Но перед тем, как будет совершён переход на следующий этап, важно несколько остановится на некотором из данных множеств.
Углубляясь в историю древних цивилизаций, можно сделать вывод что с древних времен люди ввели систему счета. В первобытные времена как можно догадаться уровень развитости людей на планете был на низшем уровне, несмотря на это они учились выживать в те суровые времена, учились охотиться, добывать еду. По древним рисункам на скалах, которые археологи находят посей день, можно сделать вывод, что система счета была неприемлемой частью жизни того народа.
Они считали: сколько (добычи) было собранно, сколько можно сегодня израсходовать, а сколько оставить до конца следующей охоты. Следовательно, множество натуральных чисел – это числа, используемые при счете. Обозначение их, как и было указано – N, и входят в это множество числа от {1,2,3,4… до бесконечности}. Множество натуральных чисел занимает первый ряд среди всех множеств чисел. Над натуральными числами можно проводить несколько арифметических операций:
Сложение (1.1):
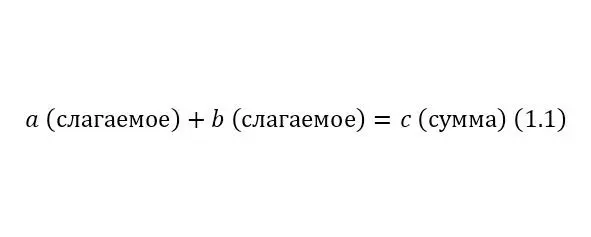
Умножение (1.2):
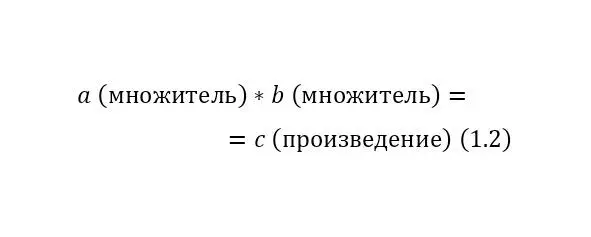
Вычитание (1.3):
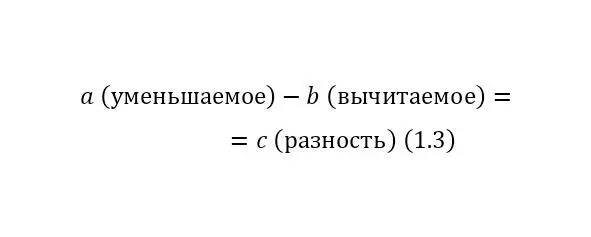
При этом уменьшаемое должно быть больше вычитаемого, иначе в результате получится отрицательное число или ноль, то есть число уже не будет принадлежать множеству натуральных чисел;
Читать дальше

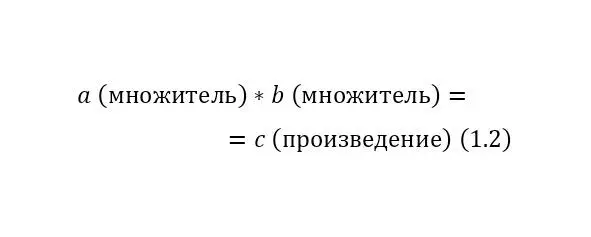
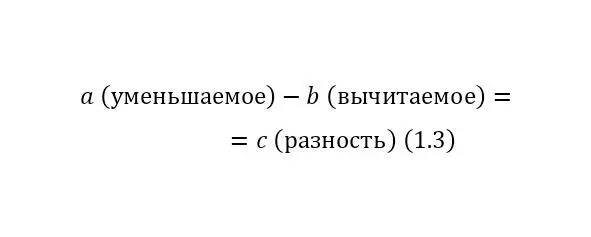



![Марат Салихов - Продажи. Простые рецепты повышения эффективности продаж от Марата Салихова [publisher - SelfPub]](/books/438102/marat-salihov-prodazhi-prostye-recepty-povysheniya-e-thumb.webp)







