Boxodir Xoshimovich - All sciences. №6, 2022. International Scientific Journal

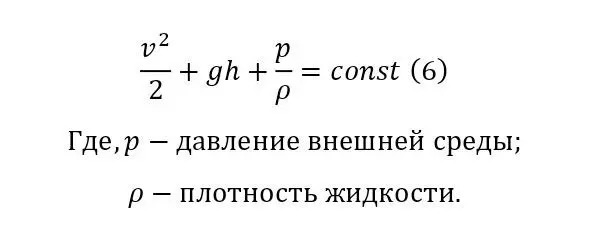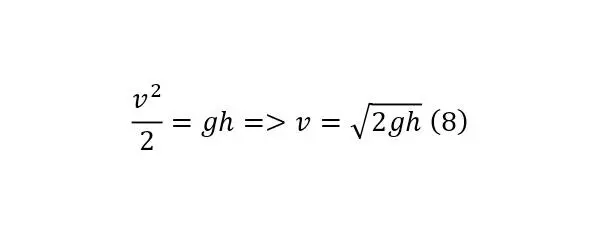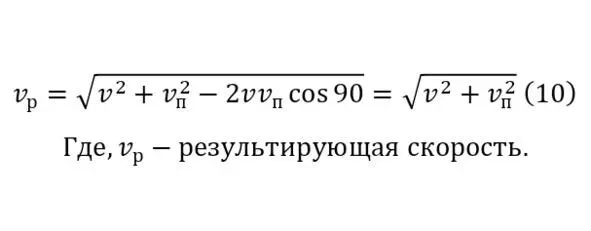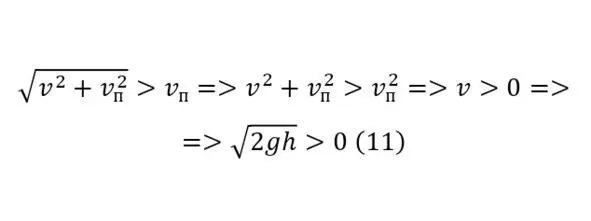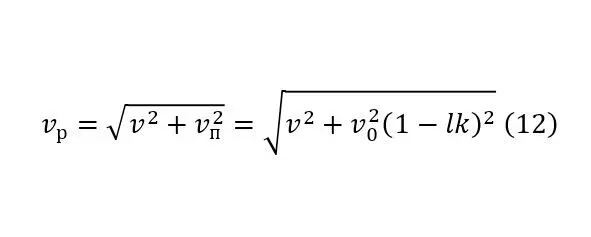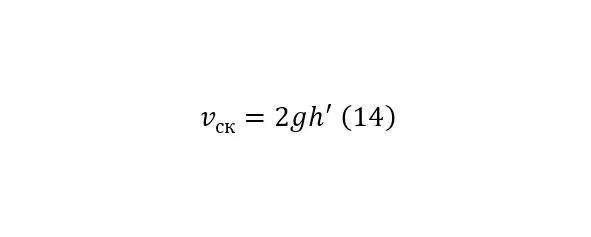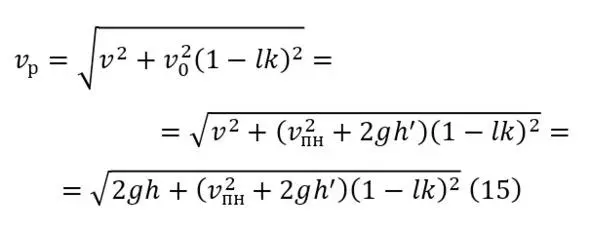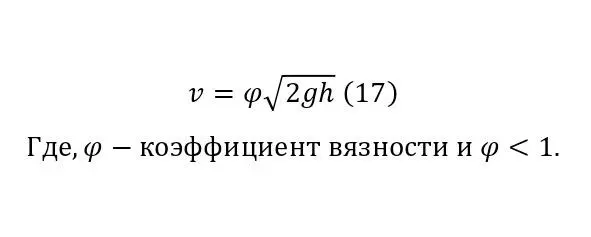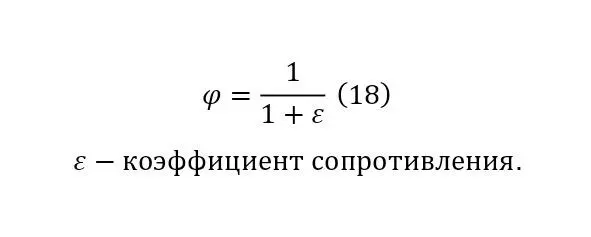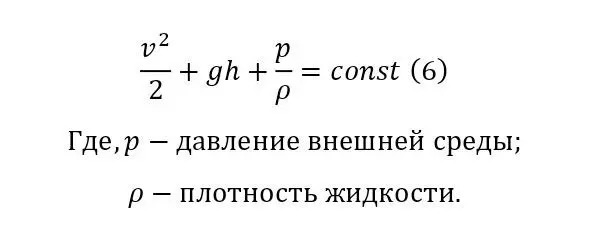
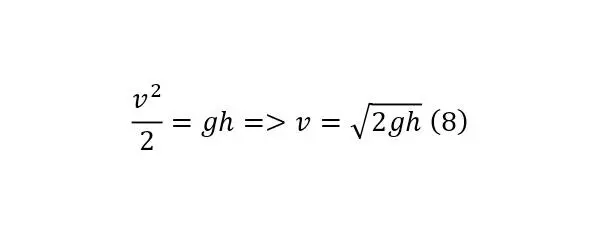
From this, it is possible to obtain a secondary additional vector, which most often prevails and makes it move under the pressure of the water itself, and the vector of the inflow velocity into the reservoir itself is most often extinguished. But when the situation is with conventional small hydropower plants, the situation is different here, since the braking capacity of the available small volume in the «dam» is not so high and is determined by the coefficient of friction of water on water, so to speak. That is, each segment, the reduction occurs precisely by the specified energy coefficient (9).

This velocity vector is summed with the resulting velocity vector due to pressure (8) at right angles forming the resulting vector (10).

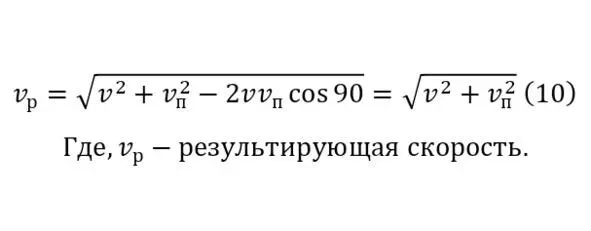
The resulting output vector will logically be larger than the initial velocity vector (11), so it can be concluded that the use of dams in the design of small hydropower plants is quite appropriate technology.

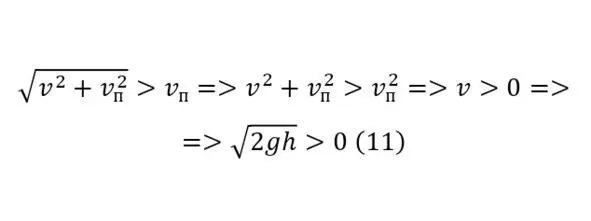
That is, no matter how small the height of the dam and its difference between the outlet of the flow and the water level, the effect, although insignificant, will be provided. It is also interesting here to determine the dependence of the initial velocity itself and the resulting vector (12).

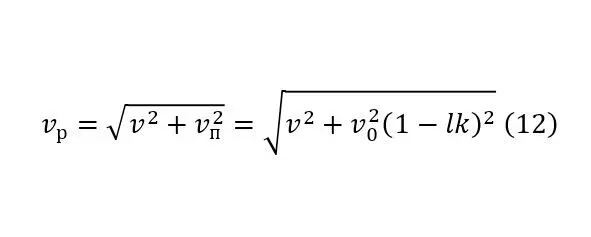
This dependence was deduced because even the initial velocity itself is not quite simple and due to the fact that the lower cavity of the ravine for the "reservoir" should be made in the form of a slope. Along with a decrease in coefficient depending on the length of this path according to (9), the initial velocity will increase, since to the initial velocity before entering the "reservoir", at which the flow had potential energy, the kinetic energy into which this potential is converted, that is, the same principle applies (1-5), but at in this case, the angular coefficient acts.

And if, since again this potential downward vector is also at an angle of 90 degrees to the main initial vector, their summed vector will be determined by (13), creating a dependence for the initial velocity on the initial one in the next location.

From where it is true (14).

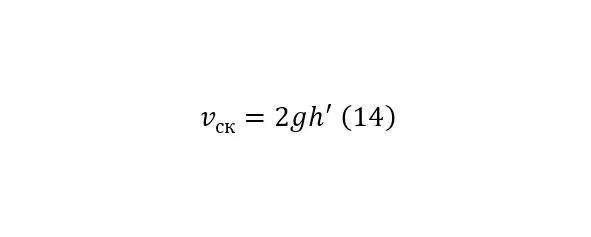
And it is important to take into account that (13) together with (14) acts only with a flat slope of the ravine itself, not counting the coefficient of friction, in the case of its calculation, an additional coefficient is included in (14), exactly as in other cases, for implementation, but this coefficient is determined empirically.

In the case of (13) and (14), the previously described (12) changes as (15).

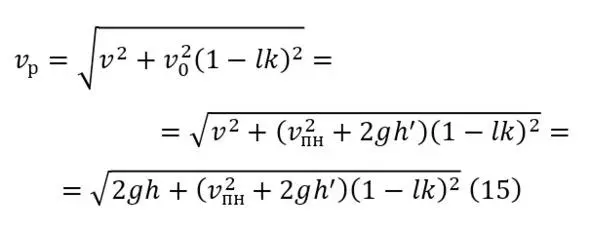
Thus (15) can be considered a full-fledged formula for the action of a straight slope at the bottom of a ravine. If there are several vectors, it is advisable to use (16), for the simple reason that several vectors will not come from the same direction, because then they can be combined into one. And the vectors may be different due to the presence of additional turns, large irregularities and similar insignificant reasons.

The final touch is only the introduction of the coefficients mentioned earlier, namely, the coefficients of a kind of viscosity (18), depending on the coefficient of resistance of movement in the flow (17).

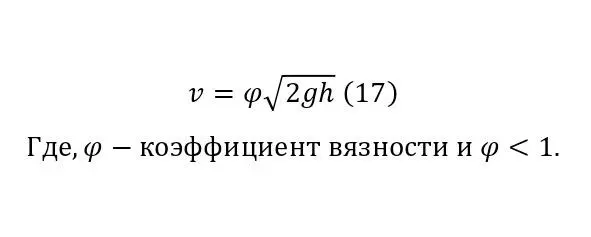
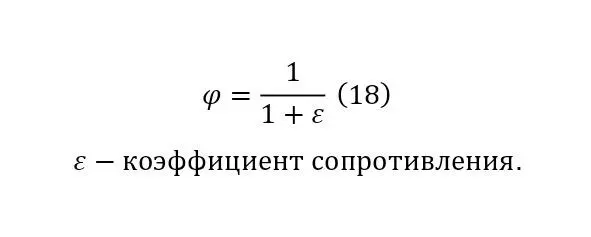
This type (17) of formula (8) was proved and described by the Italian scientist Evangelista Torricelli in 1643, and later it was shown that this formula, as already mentioned, is a consequence of Bernoulli's law.

In conclusion, it can be noted that the development of hydropower has a very progressive character, which pleases. And this development requires more and more new technologies, among which one of the best may be the technology of using a «small reservoir» or an artificial moat with an inclined bottom to increase the efficiency of the entire hydropower plant.

1. Evangelista Torricelli. De motu aquarium // Opera Geometrica. – 1644. C. 191. «Aquas violenter erumpentes in ipso eruptionis puncto eundem impetum habere, quem haberet grave aliquod, sive opsius aquae gutta una, si ex suprema eiusdem aquae superficie usque ad orificium eruptions naturaliter cecidisset».

2. Zinoviev V. A. Brief technical reference. Volume 1. – M., Gosizdat, 1949. – p. 362.

3. Savelyev I. V. Course of general physics. Volume 1. Mechanics, molecular physics. – M., Nauka, 1987. – p. 251.

Аннотация. Мақолада гидроэлектростанцияларнинг самарадорлигини ортириш бўйича фикрлар юритилинган. Сув ресурсларидан комплекс фойдаланиш хақидаги мулоҳазалар кирилиган бўлиб, шу билан биргаликда гидротармоқларда транспорт муаммосини ҳал қилишга катта ҳисса қўшилинган.

Калит сўзлар: ГЭС, самарадорлик, сув ресурслари, электр энергияси, ирригация, дарё транспорти, рекреация.