Мичио Каку - Уравнение Бога. В поисках теории всего

Точно так же красива снежинка, потому что при повороте на 60º ее форма не меняется. А сфера обладает еще большей симметрией. Ее можно повернуть вокруг центра на любой угол в любом направлении, и она будет выглядеть неизменной. Для физика уравнение красиво, если можно поменять местами его части и элементы и обнаружить, что результат не изменился, – иными словами, если видно, что между его частями имеется симметрия. Математик Годфри Харди однажды написал: «Построения математика, как построения художника или поэта, должны быть красивы ; идеи, подобно цветам или словам, должны складываться гармонично. Красота – это первоначальный тест. Для безобразной математики в мире нет постоянного места» [14]. Красота, о которой здесь идет речь, – это симметрия.

Как мы уже говорили, если взять Ньютонову силу тяготения для Земли, обращающейся вокруг Солнца, то радиус орбиты Земли будет постоянным. Координаты X и Y меняются, но радиус R остается неизменным. Это правило можно распространить и на три измерения.

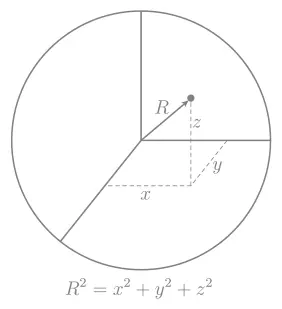
Рис. 5.Когда вы перемещаетесь по поверхности Земли, радиус Земли R остается константой, инвариантом, а ваши координаты X, Y и Z непрерывно меняются, как бы переходя друг в друга. Математическим выражением сферической симметрии является трехмерная теорема Пифагора

Представьте, что вы сидите на поверхности Земли, где ваше местоположение в трех измерениях задается тремя координатами X, Y и Z (см. рис. 5). Как бы вы ни перемещались по поверхности Земли, расстояние R от вас до ее центра останется неизменным, причем R 2= X 2 + Y 2 + Z 2. Это уравнение – трехмерный вариант теоремы Пифагора [15].

Итак, если мы возьмем уравнения Эйнштейна, а затем переведем пространство во время, а время в пространство, то уравнения останутся неизменными. Это означает, что три измерения пространства объединены теперь с измерением времени T , которое становится четвертым измерением в системе [16]. Эйнштейн показал, что величина X 2 + Y 2 + Z 2 – T 2(где время представлено в определенных единицах) остается неизменной, то есть получил модифицированный вариант теоремы Пифагора для четырех измерений. (Обратите внимание, что координата времени присутствует здесь со знаком минус. Это означает, что, хотя теория относительности инвариантна при вращении в четырех измерениях, с временем в ней обращаются немного иначе, чем с остальными тремя пространственными измерениями.) Таким образом, уравнения Эйнштейна симметричны в четырех измерениях.

Уравнения Максвелла были сформулированы примерно в 1861 г. – в год начала Гражданской войны в Америке. Они, как уже говорилось, обладают симметрией с точки зрения взаимопревращения электрического и магнитного полей. Но эти уравнения обладают еще одной, скрытой симметрией. Если мы преобразуем уравнения Максвелла в четырех измерениях, поменяв местами X, Y, Z и T , как сделал в 1910-е гг. Эйнштейн, они останутся неизменными. Это означает, что, если бы физики не были так ослеплены успехами Ньютоновой физики, теория относительности могла бы появиться еще во время Гражданской войны в США!

Хотя Эйнштейн показал, что пространство, время, вещество и энергия являются компонентами более масштабной четырехмерной симметрии, в его уравнениях оставалась очевидная прореха: в них ничего не говорилось о тяготении и ускорениях. Эйнштейна это не устраивало. Он хотел обобщить свою более раннюю теорию, которая получила название специальной теории относительности, таким образом, чтобы в нее вошли гравитация и ускоренное движение, и создать более всеобъемлющую общую теорию относительности.

Коллега Эйнштейна физик Макс Планк, впрочем, предупредил его о трудности создания теории, совмещающей относительность и тяготение. Он сказал: «Как старший друг, я должен отговорить вас от этого. Ибо, во-первых, вы не добьетесь успеха, а если даже добьетесь, никто вам не поверит». Но затем он добавил: «Если вам все же удастся это сделать, вас назовут новым Коперником» [17].

Любому физику было очевидно, что теория всемирного тяготения Ньютона и теория Эйнштейна не согласуются друг с другом. Если бы Солнце внезапно исчезло без следа, то, согласно утверждению Эйнштейна, Земля ощутила бы его отсутствие только через восемь минут. В знаменитой формуле гравитации Ньютона скорость света отсутствует. Следовательно, гравитация распространяется мгновенно, нарушая законы относительности, и Земля должна ощутить отсутствие Солнца сразу же, мгновенно.