Сергей Попов - Вселенная. Краткий путеводитель по пространству и времени - от Солнечной системы до самых далеких галактик и от Большого взрыва до будущего Вселенной

Процессы на больших красных смещениях выглядят для нас как бы растянутыми во времени.

Красное смещение соответствует изменению не только длины, но и частоты волны, так что можно говорить об изменении относительного хода времени. Если бы мы наблюдали в галактике на z = 1 часы, то увидели бы, что они идут в два раза медленнее наших. И такие часы имеются: в качестве таковых могут выступать далекие сверхновые, для некоторых из них мы умеем восстанавливать их истинные кривые блеска. Если без учета эффекта красного смещения блеск близкой сверхновой спадает, скажем, с характерным масштабом две недели, то на z = 0,5 мы будем наблюдать спад, замедленный в (1 + z) раз (т. е. в полтора раза больше – три недели). Это же верно для любого характерного временнóго процесса: на красном смещении z он кажется нам в (1 + z) раз более медленным [13] Можно эквивалентно описать это и через увеличение расстояния между, скажем, фотонами, соответствующими началу и концу вспышки, по мере распространения сигнала в расширяющейся Вселенной. Это расстояние растет так же, как длина волны, т. е. как (1 + z). .

Начиная с 1930-х гг. в течение нескольких десятилетий рассматривались альтернативные варианты интерпретации космологического красного смещения. Однако их пришлось отбросить после сравнения предсказаний этих моделей с данными наблюдений. Например, мы знаем, что величина красного смещения не зависит от длины волны (в 2016 г. точность таких наблюдений была доведена до одной миллионной), что противоречит ряду альтернативных сценариев.

Были придуманы специальные критерии (например, тест Толмена, связывающий поверхностную яркость галактик с их красным смещением), предназначенные для проверки предсказаний разных моделей. Оказалось, что поверхностная яркость галактик спадает в строгом соответствии с предсказаниями стандартной космологической модели (в 1930 г., когда был предложен тест, она еще не была таковой).

Для наблюдений нам доступна лишь конечная область – часть большой Вселенной. Астрономические данные свидетельствуют в пользу того, что наблюдаемая часть пространства в больших масштабах однородна и изотропна. Это является основой наших представлений о геометрии Вселенной. При этом все выводы о параметрах большой Вселенной являются экстраполяцией.

Вселенная может быть конечной или бесконечной (ее объем может быть конечным или бесконечным), при этом конечность Вселенной не подразумевает наличия какой-либо границы. Современное понимание этой ситуации восходит к работам Бернхарда Римана (Georg Friedrich Bernhard Riemann), который впервые описал конечное, но безграничное пространство положительной кривизны. В любом случае у нас нет однозначных данных в пользу какой-то из этих двух альтернатив.

Наша Вселенная выглядит однородной, изотропной и плоской.

Геометрия Вселенной характеризуется еще несколькими параметрами. Изучать топологию (форму) Вселенной довольно сложно, поскольку нам доступна для наблюдений лишь малая ее часть. А вот кривизна пространства Вселенной – гораздо более перспективный предмет исследований.

Мы не видим никаких свидетельств в пользу конечности Вселенной или ее нетривиальной топологии.

Пространство может иметь положительную кривизну, нулевую (плоское пространство) и отрицательную. В пространстве положительной кривизны через точку, не лежащую на данной прямой, нельзя провести ни одной прямой, не пересекающейся с данной (вспомните, как сходятся меридианы на сфере), а суммы углов треугольников (на космологических масштабах) будут больше 180°. В пространстве нулевой кривизны (евклидова геометрия) через точку вне прямой можно провести только одну прямую, не пересекающуюся с данной, и сумма углов треугольника равна 180°. В пространстве отрицательной кривизны (геометрия Лобачевского) мы можем провести через точку сколько угодно прямых, которые никогда не пересекутся с данной, а сумма углов большого треугольника будет меньше 180°. В космологии эти три случая можно связать с величиной средней плотности Вселенной, плоскому пространству соответствует определенная критическая плотность.

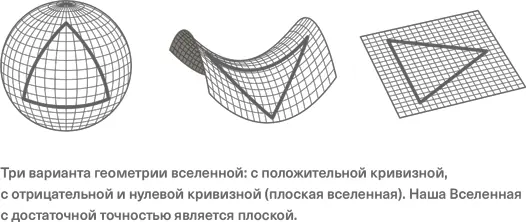
Наилучшие на сегодняшний день измерения геометрии Вселенной проведены с помощью наблюдения реликтового излучения (см. главу 12 «Реликтовое излучение»). Из этих наблюдений можно с высокой точностью определить отношение размера «звукового горизонта» (горизонта для распространяющихся колебаний в среде) на момент последнего рассеяния к расстоянию до источника реликтовых фотонов на момент их излучения, плюс нам известно значение красного смещения, соответствующее эпохе рекомбинации (z = 1100). Во вселенных разной кривизны линейный размер, соответствующий звуковому горизонту на z = 1100, имел бы на небесной сфере разные угловые масштабы. Данные показали, что в пределах ошибок (с точностью лучше процента) геометрия Вселенной – плоская. Конечно, наша Вселенная трехмерна, и, говоря о том, что она «плоская», мы имеем в виду применимость евклидовой геометрии для Вселенной в большом масштабе.