Стивен Габсер - Маленькая книга о черных дырах [litres]

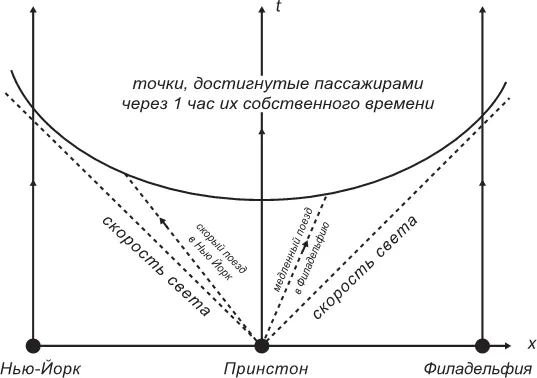
Рис. 1.2.Поезда, отправляющиеся из Принстона. Кривая, объединяющая точки, в которые пассажиры попадают через час собственного времени, – гипербола.

В пространстве-времени Минковского постоянную скорость света мы визуализируем световыми лучами под углом ровно 45° относительно вертикальной оси времени. Можно заметить, что гипербола, образованная всеми возможными конечными пунктами наших одночасовых путешествий, целиком лежит внутри области пространства-времени, ограниченной двумя световыми лучами, выходящими из начала координат. Так в пространстве-времени Минковского отражается тот факт, что никакой поезд не способен двигаться быстрее света. Может показаться, что наши разговоры о замедлении времени не имеют отношения к преобразованиям Лоренца. Сейчас мы покажем, что это совсем не так. Вспомним, что мы когда-то решили назвать систему отсчета поезда системой А , а систему отсчета, связанную с Землей, – системой Б . Пусть Алиса проводит один час в системе А по дороге из Принстона в Нью-Йорк. А тем временем Боб и его друзья остаются неподвижными по отношению к Земле. Как они могут узнать время прибытия Алисы? Может, ей стоит позвонить им с вокзала? Вряд ли это разумно: ведь радиоволны, несущие ее голос, распространяются со скоростью света, а значит, чтобы узнать время ее прибытия, Бобу и его друзьям придется проделать вычисления, в которых надо будет учесть время приема звонка Алисы, скорость распространения сигнала и расстояние до Нью-Йорка. Так как Бобу лень заниматься такими сложными подсчетами, он придумывает лучший способ: он сверяет – синхронизирует – свои часы с часами своего друга Билла. Затем Боб и Билл выбирают себе позиции на платформах в Принстоне и Нью-Йорке соответственно, и Боб засекает время отправления Алисы, а Билл – время ее прибытия. Нужды в телефонном звонке больше нет. Правда, может показаться, что трудно надежно синхронизировать часы у наблюдателей, далеко расположенных друг от друга. Для этого можно предложить следующий способ: Боб и Билл встречаются на полпути между Принстоном и Нью-Йорком, синхронизируют свои часы в одной и той же точке пространства, а потом с одинаковой скоростью отправляются на свои вокзалы, задолго до того, как Алиса садится в свой поезд. Во всей этой истории с поездкой Алисы система А оказывается в явно привилегированном положении: Алиса не нуждается в помощи друзей, чтобы узнать продолжительность своего путешествия, тогда как Боб и Билл должны для измерения этого времени производить сложные совместные действия. Временной интервал, который измеряет Алиса, называется «собственным временем», так как она измеряет его, оставаясь неподвижной в своей системе отсчета (системе А ). А временной интервал, который измеряют Боб и Билл, – назовем его «замедленным временем», – всегда будет больше собственного. Замедленное, или растянутое, время и есть выражение связи между системой А и системой Б в пространстве-времени. Преобразование Лоренца при переходе от системы А к Б содержит замедление времени.

Подобным образом можно описать и сокращение длины. Теперь вместо надоевших уже прогулок в поездах давайте представим себе, что Боб, Билл и Алиса едут на Олимпиаду, где Алиса надеется установить мировой рекорд по прыжкам с шестом. Ее секрет в том, что она умеет очень быстро бегать: со скоростью в 87 % скорости света! (Почему-то она при этом не хочет отбирать лавры Усейна Болта на стометровке, хотя знает, что эту дистанцию она преодолеет менее чем за 0,4 микросекунды.) У Алисы шест длиной 6 метров – это длиннее, чем у большинства прыгунов, но что поделаешь, она во всем исключительная. Боб и Билл не верят, что у Алисы такой длинный шест, и они решают измерить его, пока Алиса разбегается для прыжка, держа при этом свой шест строго горизонтально. Ясное дело, задача у них непростая. Как им провести свои измерения? Вот что они придумали: во-первых, они опять синхронизуют свои часы. Затем они становятся на расстоянии немного меньше шести метров друг от друга и договариваются, что точно в одно и то же время, когда Алиса будет пробегать мимо них, они посмотрят на нее и отметят, какую точку шеста видит каждый. После многих попыток им удается добиться такого положения, при котором Боб видит конец шеста в тот момент, когда Билл видит его острие. Они измеряют расстояние между собой, и оказывается, что они стоят всего в 3 метрах друг от друга, из чего они разумно заключают: длина шеста Алисы всего 3 метра. Но когда они подходят к Алисе и рассказывают ей об этом, та возражает. Позвав на помощь двух своих друзей Аллана и Авери, которые бегут рядом с ней (а они такие же замечательные спринтеры, как и сама Алиса), и измерив длину шеста в своей собственной системе координат, она подтверждает, что эта длина равна 6 метрам.