Герман Смирнов - Под знаком необратимости (Очерки о теплоте)

По-разному комбинируя эти процессы, нетрудно получить теоретические циклы, по которым работают современные тепловые двигатели. Скажем, комбинация из двух адиабатических и двух изохорных процессов образует цикл бензинового двигателя. Если заменить в этом цикле изохорный процесс, по которому идет нагрев газа, изобарным, можно получить цикл Дизеля. Два адиабатических и два изобарных процесса дадут теоретический цикл газовой турбины. Кстати, по этому же циклу работает и металлический стержень, поднимающий груз. Два изотермических и два изобарных процесса складываются в цикл Эриксона, а два изотермических и два изохорных — в цикл Стирлинга. Из всех возможных циклов Карно считал наиболее простым для анализа цикл, состоящий из двух изотерм и двух адиабат…

Он исходил из того, что в его распоряжении есть огромный источник тепла — нагреватель и столь же огромный приемник тепла — холодильник. Мы не случайно подчеркиваем, что нагреватель и холодильник огромны: благодаря этому их температура остается постоянной независимо от количества отдаваемого и получаемого тепла. Между таким изотермическим источником и приемником можно расположить тепловые машины, работающие по всевозможным циклам. Каждый из них будет превращать теплоту в работу. Но с одинаковым ли успехом? Есть ли среди этих циклов наилучший? И если есть, то какой именно?

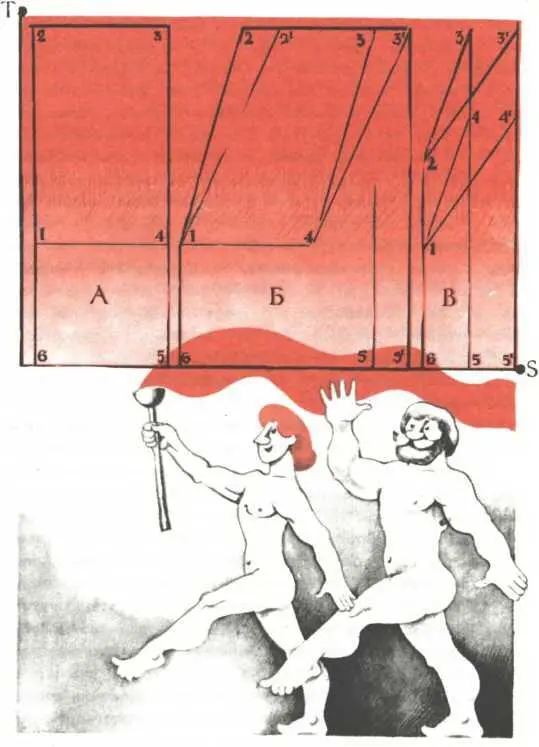
Объединив свои усилия, попеременно на все лады сжимая, нагревая, расширяя и охлаждая газ в цилиндре под поршнем, Силач и Огнепоклонник легко получили основные типы тепловых двигателей.

А — идеальный цикл Карно: 1–2 — адиабатическое сжатие, 2–3 — изотермическое расширение, 3–4 — адиабатическое расширение, 4–1 — изотермическое сжатие. Площадь 6-2-3-5 — подведенная в цикле теплота, площадь 6-1-4-5 — отведенная теплота. Площадь 1-2-3-4 — полезная работа двигателя. КПД = пл.1-2-3-4/пл.6-2-3-5.

Б — идеальные циклы Стирлинга и Эриксона.

ЦИКЛ СТИРЛИНГА (6-1-2-3-5): 1–2 — изохорное нагревание, 2–3 — изотермическое расширение, 3–4 — изохорное охлаждение, 4–1 — изотермическое сжатие. Площадь 6-1-2-3-5 — подведенная теплота, площадь 6-1-4-3-5 — отведенная теплота. Площадь 1-2-3-4 — полезная работа. КПД = пл.1-2-3-4/пл.6-1-2-3-5.

ЦИКЛ ЭРИКСОНА (6-1-2'-3'-5'): 1–2' — изобарное нагревание, 2'-3' — изотермическое расширение, 3'-4 — изобарное охлаждение, 4–1 — изотермическое сжатие. Площадь 6-1-2'-3'-5' — подведенная теплота, площадь 6-1-4-3'-5' — отведенная теплота. Площадь 1–2'-3'-4 — полезная механическая работа. КПД = пл.1–2'-3'-4/пл.6-1-2'-3'-5'.

В — идеальные циклы Отто и Брайтона.

ЦИКЛ ОТТО (6-2-3-5): 1–2 — адиабатическое сжатие, 2–3 — изохорный нагрев, 3–4 — адиабатическое расширение, 4–1 — изохорное охлаждение. Площадь 6-2-3-5 — подведенная теплота, площадь 6-1-4-5 — отведенная теплота. Площадь 1-2-3-4 — полезная механическая работа. КПД = пл.1-2-3-4/пл.6-2-3-5.

ЦИКЛ БРАЙТОНА (6-2-3'-5'): 1–2 — адиабатическое сжатие, 2–3' — изобарный нагрев, 3'-4' — адиабатическое расширение, 4'-1 — изобарное охлаждение. Площадь 6-2-3'-5' — подведенная теплота, площадь 6-1-4'-5' — отведенная теплота. Площадь 1-2-3'-4' — полезная механическая работа. КПД = пл.1-2-3'-4'/пл.6–2—3'—5'.

Карно считал, как уже говорилось раньше: «в телах, употребляемых для развития движущей силы тепла, не должно быть ни одного изменения температуры, происходящего не от изменения объема». Это значит, что в цикле не должно быть ни одного процесса, в котором рабочее тело изменяло бы свою температуру за счет подвода или отвода теплоты.

Изменять температуру можно лишь за счет адиабатических, чисто механических процессов. А подвод или отвод тепла в изотермических процессах не сопровождается изменением температуры. Вот почему цикл, составленный из двух адиабатических и двух изотермических процессов, будет самым эффективным из всех, могущих быть встроенными между изотермическим нагревателем и холодильником.

Чтобы сравнить двигатели, работающие по разным циклам, их экономичность оценивается с помощью числового коэффициента — коэффициента полезного действия, который для тепловых двигателей представляет собой отношение работы, полученной на выходе, к теплоте, подведенной на входе. Этот коэффициент — КПД — для идеального цикла Карно выражается очень простой формулой: КПД = Т 1- Т 2/Т 1.

Здесь Т 1— абсолютная температура нагревателя, а Т 2— абсолютная температура холодильника. (Абсолютная температура получается прибавлением 273,16° к температуре по шкале Цельсия.)