Лоуренс Краусс - Таємниці походження всесвіту

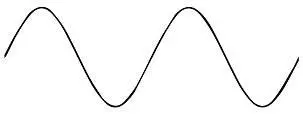
Як уже було зазначено вище, у квантовій механіці частинки мають хвилеподібну природу. Завдяки Максу Борну ми знаємо, що квадрат амплітуди хвилі, пов’язаної з частинкою в довільній точці, – услід за Шрьодінґером ми називаємо це хвильовою функцією частинки, – визначає ймовірність виявлення частинки в цій точці. Оскільки амплітуда наведеної вище коливної хвилі більш-менш однакова на всіх піках, така хвиля, якщо вона відповідає ймовірнісній амплітуді виявлення електрона, означатиме більш-менш однорідно розподілену ймовірність виявлення електрона будь-де на її шляху.

Тепер поглянемо, як виглядатиме збурення, якщо воно є сумою двох хвиль із дещо різними частотами (довжинами хвилі), що рухаються вздовж осі х :

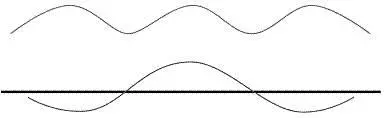
Поєднавши ці дві хвилі, дістанемо таке збурення:

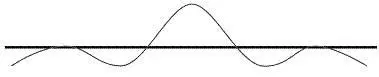
Через деяку відмінність довжин цих двох хвиль піки й западини будуть скасовувати одне одного, або «негативно інтерферувати» всюди, окрім невеликої кількості місць, де в одній точці сходитимуться два піки (одне з таких місць показане на рисунку вище). Це нагадує феномен інтерференції хвиль в описаному раніше експерименті Юнґа з двома щілинами.

Якщо додати ще одну хвилю з дещо іншою довжиною,

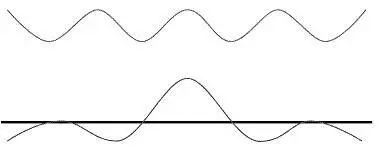
результуюча хвиля виглядатиме так:

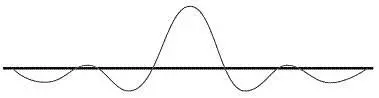
Інтерференція стирає ще більше коливань, за винятком ділянки, де дві хвилі збігаються, за рахунок чого амплітуда хвилі в піку значно більша, ніж деінде.

Можна уявити, що станеться, якщо продовжити цей процес, додаючи до початкової хвилі чітко вивірену кількість хвиль із дещо різними частотами. Урешті-решт амплітуди результуючої хвилі скорочуватимуться всюди, крім деякого невеликого околу в центрі фігури та віддалених місць, де знову можуть зійтися всі піки.

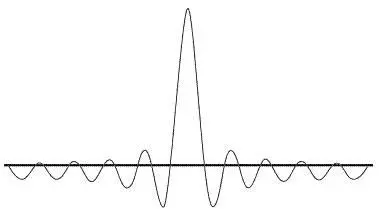
Чим більше дещо відмінних частот буде складено докупи, тим вужчим буде найбільший центральний пік. Тепер уявімо, що це є представленням хвильової функції деякої частинки. Чим більшою є амплітуда центрального піка, тим вища ймовірність виявити частинку десь у межах ширини цього піка. Проте ширина центрального піка ніколи не досягає нуля, тож збурення лишається розподіленим по деякій малій, хоча й дедалі вужчій ділянці.

Тепер згадаймо, що Планк та Ейнштейн розповіли нам, що принаймні у випадку світлових хвиль енергія кожного кванта випромінювання, тобто кожного фотона, прямо пов’язана з його частотою. Не дивно, що аналогічне співвідношення справедливе для ймовірнісних хвиль, пов’язаних із масивними частинками, проте в цьому випадку з частотою асоційованої з такою частинкою ймовірнісної хвилі пов’язаний імпульс цієї частинки.

Отже, маємо відношення невизначеності Гайзенберга: якщо ми хочемо локалізувати частинку в малій ділянці, себто зробити найвищий пік її хвильової функції якомога вужчим, ми маємо врахувати, що ця хвильова функція отримана шляхом комбінування великої кількості різних хвиль із дещо різними частотами. Але це означає, що імпульс цієї частинки, який пов’язаний із частотою її хвильової функції, має бути дещо розподілений. Чим вужчим у просторі є домінантний пік хвильової функції частинки, тим більшу кількість різних частот (себто імпульсів) треба скласти докупи, щоб утворити кінцеву хвильову функцію.

Якщо простіше, чим точніше ми бажаємо встановити конкретне місцезнаходження частинки, тим більшою стає невизначеність її імпульсу.

Як бачите, тут нема ніяких обмежень, пов’язаних із реальними спостереженнями, зі свідомістю, чи з конкретною технологією, пов’язаною з якимсь спостереженням. Невід’ємною властивістю фактичного стану справ є те, що у квантовому світі з кожною частинкою пов’язана якась хвильова функція, і в частинок із певним фіксованим імпульсом хвильова функція має певну специфічну частоту.