В. Уральцев - Матрица физики, законов природы

Обратимся к выражению R 3/T 2 . Умножим это соотношение на постоянный коэффициент, равный 4π 2 . Получаем: 4π 2R 3/T 2 .

Эта формула приводится в учебниках физики для расчетов массы Солнца, но в ней отсутствует еще один множитель – постоянная Кавендиша. Этот множитель необходим только для перевода размерности L, T (метр, секунда) в килограммы (тонны).

Третий закон Кеплера в нашей трактовке принимает вид:

4π 2R 3/T 2=m Солнца (размерность здесь и далее L, T).

Но в этом случае, подчеркнем, если величину 4π 2R 3/T 2 , где R -расстояние от Земли до Солнца (м), а Т – время одного оборота Земли вокруг Солнца (с), разделить на квадрат скорости движения Земли по орбите вокруг Солнца, получим R – расстояние от Земли до Солнца. В свою очередь, если разделить значение этого расстояния еще раз на величину скорости, то получим время одного оборота Земли вокруг Солнца, деленное на 2π .

Естественно, что эти расчеты можно провести, подставив величины R и Т , соответствующие движению любой другой планеты по своей орбите. Пытливому читателю предоставлена возможность провести эти расчеты самостоятельно.

На основании изложенного можно сделать вывод, что массу Солнца формирует динамика вращательного движения. Ведь в формуле не участвует значение массы планет!

Перейдем ко второму закону движения планет И. Кеплера и попытаемся определить его сущность. Для этого обратимся к вихрю. Да, к тому самому вихрю, который мы часто наблюдаем на улицах и площадях своих городов, в парках или в поле. Его разновидности – тайфуны и торнадо – нам показывают по телевидению. Вихрю посвящены сотни статей в научно-популярной и специальной литературе.

В специальной литературе по аэро- и гидродинамике приводится формула движения частицы в плоском вихре: RV=соnst . Это выражение можно сформулировать так: при вращении вихря радиус-вектор движущейся точки заметает равные площади в единицу времени:

R2πR/T=соnst , м 2/с

Таким образом, мы математической формулой выразили второй закон И. Кеплера. Квантованием получаем ряд:

4π 2R 3/T 2 , м 3/с 2 – масса Солнца. (Третий закон И. Кеплера).

2πR 2/T , м 2/с – площадь, заметаемая радиус-вектором в единицу времени. (Второй закон И. Кеплера).

R ,м – радиус движения точки вихря.

Т/2π , с – время одного оборота точки вихря.

Единицей квантования данного ряда является линейная скорость движения точки данного вихря или любой планеты Солнечной системы.

В этом ряду формул чувствуется определенная закономерность!

Чтобы продолжить наши исследования, нам необходимо обратиться к работам нашего современника, человека необычной судьбы – Роберта Людвиговича Бартини.

Сын богатого итальянского барона-аристократа, он ни в чем не знал отказа: собственные яхты и вилла на берегу Адриатики, громадная библиотека отца, где мальчик зачитывался сочинениями Вольтера, Руссо, Дидро. В начале Первой мировой войны Бартини попадает в плен к русским. По возвращении в Италию экстерном заканчивает Миланский политехнический институт. С приходом к власти Муссолини Бартини покидает Италию и возвращается в Россию, где становится видным авиаконструктором. Известны его скоростные, на то время, самолеты «Сталь-6» и «Сталь-7» [7, 23].

Но нас будут интересовать не самолеты Бартини, а Таблица «Система пространственно-временных величин»

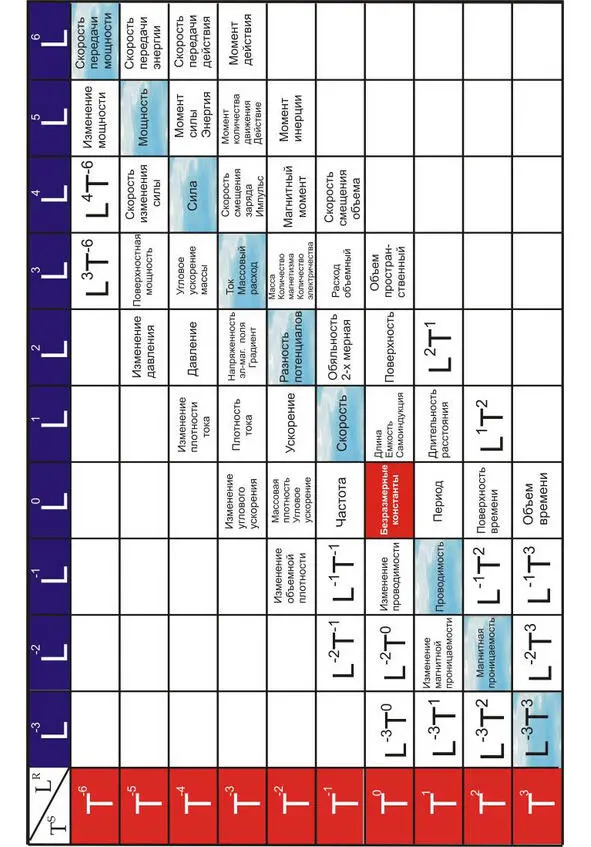
,предложенная им совместно с П. Кузнецовым. Она состоит из вертикальных столбцов, представляющих собой целочисленные степени длины L и горизонтальных строк – целочисленных степеней времени Т. Пересечение каждого столбца и каждой строки автоматически дает размерность той или иной физической величины. Авторы пытались максимально заполнить клеточки таблицы известными физическими величинами.

Однако таблица не была привязана к физической реальности, она не имела ни одной математической формулы для выполнения анализа системы.

Автор, совместно с Волкевичем И. Ф. предлагают таблицу, построенную по тому же принципу, но заполненную математическими формулами. Она называется «Таблица формул для расчетов преобразований во вращательном и колебательном движениях».

В нее прекрасно вписываются законы И. Кеплера. Таблица полна гармонии. По сути, мы имеем дело с одной формулой, ядром всей таблицы: R nV m . Основой таблицы является столбец М 0 и строка С 0 . На их пересечении находится безразмерная единица. Почему? На этот вопрос пока ответа нет. Всего в таблице 56 клеточек, из них 7 – от индуктивности R 1V -2 до энергии R 1V 4 – являются основными, которые определяют параметры процесса вращения любой планеты Солнечной системы вокруг Солнца: