Александр Астахов - Физика движения. Альтернативная теоретическая механика, или Осознание знания. Книга в двух томах. Том I

Так что не стоит слепо верить мнениям, даже авторитетным. Правильно говорил Козьма Прутков, что если на клетке слона прочтешь «буйвол», не верь глазам своим!

Но позвольте, если Галилей не проводил опытов по бросанию шаров с наклонной Пизанской башни, то откуда его доказательство, что быстрота падения тел не зависит от их тяжести?

Доказательство это построено на формальной логике, и, на взгляд автора, это чистой воды софистика. Посудите сами, вот цитата из Галилея: «Уважаемые сеньоры, представьте, что вы взошли на башню, имея две монеты в 5 и 3 скудо. Первая должна падать быстрее, вторая – медленнее. Если вы свяжете монеты бечевкой, вес возрастет, и они должны падать быстрее, но, с другой стороны, монета в 3 скудо, как более легкая, должна тормозить 5 скудо. Получаемое противоречие снимается одним утверждением – вес предмета не влияет на скорость свободного падения».

Давайте задумаемся, какое падение Галилей имел в виду: в воздухе или пустоте? Конечно, в воздухе, потому что пустота, или вакуум, был открыт только его учеником Торричелли, причем гораздо позже; да и никому в голову еще долго после этого не могла прийти мысль бросать тела в пустоте – об аэродинамике тогда не имели понятия, а пустота существовала только в крохотном верхнем конце трубочки ртутного барометра Торричелли. Но тогда быстрее всего будет падать монета в 5 скудо, медленнее – связка из двух монет, а наиболее медленно – монета в 3 скудо, причем в связке эта последняя аэродинамическим сопротивлением будет именно тормозить монету в 5 скудо. Таким образом, рассуждение Галилея неверно, можно сказать, «скудно».

А теперь послушайте предложенное автором доказательство того, что тяжелые тела падают быстрее легких, и опровергните, если можете: «Представьте себе, что вы взошли на башню, имея две матрешки: большую тяжелую, и маленькую полегче. При этом большая падает быстрее меньшей – так выбраны массы и аэродинамика этих матрешек. Если мы вложим меньшую в большую, то полученное тело будет падать быстрее всего, так как большая матрешка „берет на себя“ все аэродинамические сопротивления, в этом можно убедиться экспериментально. Значит, тяжелые тела падают быстрее легких».

Что же произойдет в пустоте или вакууме? И в первом (Галилеевом), и во втором (автора) случаях связка монет или две матрешки упадут на Землю быстрее, чем эти тела порознь, причем более тяжелое тело упадет быстрее. Почему – уже было сказано выше.

Что же касается падения тел в так называемой трубке Ньютона, то тут, простите, все правильно (рис. 36). И дробинка, и пушинка приземлятся в вакууме одновременно, потому что летят вместе, притягивая к себе Землю совместно, общей массой. А вот попробуйте сбросьте на Землю легкий астероид с высоты Луны, а потом и саму Луну (предварительно остановив ее, конечно, и убрав с земли астероид, для точности!) И измерьте разницу во времени падения, которую, кстати, несложно вычислить. А потом и говорите, кто прав: Аритотель или Галилей!

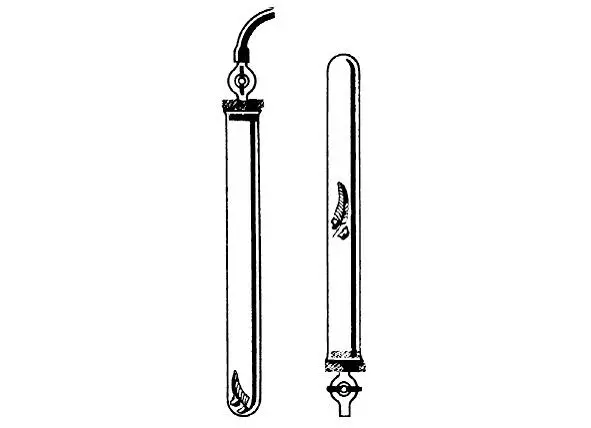
РИС. 36. ТРУБКА НЬЮТОНА»

Совершенно очевидно, что Аристотель имел в виду падение тел в условиях земной атмосферы. С этим согласен и сам профессор Гулиа, т.к. он пишет, что в «…этом может легко убедиться каждый из нас, даже не выходя из комнаты». А раз так, значит, Аристотель был абсолютно прав, что «…легкие тела падают медленнее тяжелых», но только в атмосфере. Гулиа же ссылаясь на Аристотеля, считает, что тяжелые тела и в атмосфере и в вакууме падают быстрее легких, если их бросать порознь.

Современный нам профессор физики, абсолютно необоснованно считает, что слова Галилея «…легкие, и тяжелые тела падают совершенно одинаково» следует расценивать именно как одинаковое время падения легких и тяжелых тел, выброшенных из окна порознь. Поэтому Гулиа решил поправить древнего мыслителя. Он же теперь ничего не сможет возразить «светилу» современной науки, который считает себя вправе без всяких на то оснований поправлять даже самого Ньютона, причём в ничего не значащих для науки мелочах.

Нам же кажется более очевидной версия, в соответствии с которой Галилей имел в виду ускорение падения легких и тяжелых тел, которое не зависит от их массы, как при синхронном падении, так и при раздельном падении, если масса ответного тяготеющего тела остается при этом неизменной.