Александр Астахов - Физика движения. Альтернативная теоретическая механика или осознание знания

Однако это соотношение справедливо для равномерно деформированного тела, в котором установившаяся статическая деформация равномерно распределена по его объёму для постоянной силы, вызывающей деформацию. При движении под действием постоянной силы с постоянным ускорением деформация и силы упругости распределяются неравномерно по длине тела. При этом общее удлинение по-прежнему прямо пропорционально силе и наоборот, т.е. средняя сила, действующая на каждый массовый элемент, по-прежнему обратно пропорциональна массе, что и обеспечивает закон сохранения импульса. Но если учесть, что в реальном взаимодействии сила в центре зоны деформации не постоянная, а изменяется пропорционально удлинению, то индивидуальная сила, приложенная к каждому массовому элементу в каждом поперечном сечении тела, оказывается пропорциональной квадрату удлинения. Покажем это графически на Рис. 1.2.1.

Разобьем два взаимодействующих тела, представляющие собой цилиндрические стержни с одинаковой для простоты массой и одинаковыми геометрическими размерами на равные линейные части по длине цилиндров. Пусть для простоты таких частей будет три в каждом теле. Тогда любая сила, действующая на такие тела, будет пропорциональна (кратна) трём:

Во-первых,потому что каждое тело будет состоять из трёх одинаковых связанных между собой и потому одинаково ускоряющихся под действием любой силы масс.

А, во-вторых,потому что общее удлинение таких тел так же будет пропорционально трём.

Можно взять четыре сечения. Тогда сила, зависящая от количества сечений, будет условно равна 4F, а удлинение, так же зависящее от количества сечений условно равно (х = 4) и т. д.

Пусть, исходя из нашего разбиения, при разгоне тел к ним условно приложена внешняя постоянная по величине и направлению сила равная (3F). Во время разгона к каждому элементу взаимодействующих тел будут приложены силы, показанные на соответствующей части Рис. 1.2.1. На рисунке показаны также силы, действующие между элементами. После окончания разгона тела приобретут некоторую скорость (V).

Мы не можем количественно оперировать с нулевыми или бесконечно малыми силами и удлинениями. Поэтому за точку отсчёта условно примем удлинение (х = -1) и силу (F = 1F). Эти параметры будут обозначать начало сжатия и конец расширения зоны деформации (см. Рис. 1.2.1). При этом численные значения удлинения и силы на этих стадиях могут быть сколь угодно малыми. Целесообразность их малости для практических расчётов покажет опыт. Тогда эта величина может быть принята за единичное удлинение, а сила, вызывающая её – за единичную силу. Количество сечений рассчитывается как частное от деления максимальной силы на минимальную. При этом наибольшее удлинение также будет кратно этому соотношению

И ещё одно предварительное пояснение. Сила взаимодействия образуется в самом центре зоны деформации. Эту часть зоны деформации для простоты будем условно считать несоизмеримо малой по сравнению с деформацией, распространяющейся по длине тел. Тогда за удлинение, участвующее в расчётах силы, действующей на внешних концах и в центре зоны деформации тел, будем принимать только удлинение самих тел.

Но как бы ни была мала центральная зона деформации, она также подчиняется закону Гука. А поскольку она образуется из того же материала, из которого состоят и сами тела, то сила которая в ней образуется также меняется пропорционально удлинению. Таким образом, опуская это удлинение в общем удлинении тел, мы, тем не менее, будем учитывать вызываемое им изменение силы в центре взаимодействия.

Итак, смотрим рисунок:

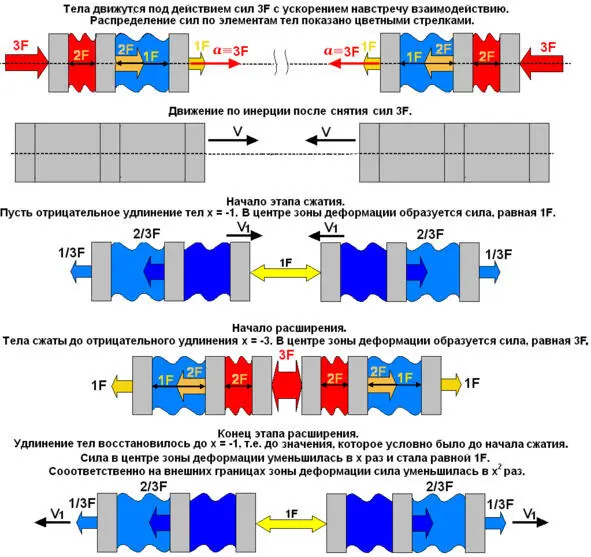
Рис. 1.2.1

В современной физике считается, что силы упругости имеют электрическую природу. Но силы Кулона как раз и имеют квадратичную зависимость от расстояния. А вот почему квадратичная зависимость кулоновских сил от расстояния превращается в линейную зависимость сил упругости от расстояния, классическая физика не поясняет. Покажем, как это может быть согласовано.

Как видно из рисунка в центре зоны деформации сила изменяется пропорционально удлинению в нашем случае в (х = 3) раз, а затем к краям зоны деформации ещё во столько же раз, т.е. всего в ((х = 3) 2) раз. То есть сила инертного взаимодействия при движении тел с переменным ускорением под действием изменяющейся силы пропорциональна квадрату удлинения зоны деформации.