Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

С другой стороны, если молекула жидкости предпочитает своих собратьев молекулам стола, силу F 1следует нарисовать больше F 2и картина примет такой вид, как на фиг. 121, где показан большой краевой угол. Для «водоотталкивания», по-видимому, требуется, чтобы молекулы жидкости испытывали со стороны соседних молекул стола меньшее притяжение, чем со стороны соседних молекул жидкости.

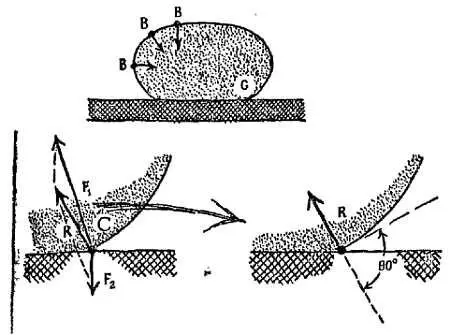
Фиг. 121. Силы, действующие на молекулу, находящуюся на краю небольшой лужицы жидкости.

Лужица находится на столе, который слабо притягивает молекулы жидкости.

Водоотталкивание и смачивание

Таково молекулярное объяснение смачивания и краевого угла.

Объяснение? Разве это не просто волшебная сказка, выдуманная для того, чтобы свести концы с концами? Нет, это объяснение совсем не так плохо, поскольку оно основано на молекулярных представлениях, которые используются в других областях физики и химии. Кроме того, оно позволяет сделать полезные рекомендации:

1) Для улучшения смачивания (мечта прачек) надо сделать F 2больше, чем F 1, т. е. надо, чтобы молекулы жидкости притягивались твердым телом сильнее, чем своими соседями. Это можно осуществить, применяя молекулы-посредники, которыми на практике являются молекулы мыла. Таким образом, мы раскрыли секрет мыла и указали путь к созданию новых синтетических моющих средств.

2) Чтобы увеличить краевой угол (надежда изготовителей плащей), надо покрыть текстильное волокно каким-либо веществом, для которого F 2мало по сравнению с F 1. На вопрос: «Какой толщины должно быть покрытие?» (еще одна забота изготовителей плащей) — примечание на стр. 195 отвечает, что достаточно очень тонкого слоя, толщиной в несколько молекул. (На вопрос: «Какова толщина молекулы?» — дан ответ в этой главе.)

3) В тех случаях, когда роль поверхностных сил велика, жидкость с небольшим краевым углом ( F 2больше F 1) будет расползаться вдоль твердой поверхности, даже карабкаясь вверх. Это особенно заметно, когда жидкости поднимаются в очень узких трубках; «капиллярность» — полезное свойство жидкостей, и мы сейчас его разберем.

Капиллярность

ДЕМОНСТРАЦИОННЫЙ ОПЫТ

Опыт 12.Нагрейте кусок стеклянной трубки, растяните его в очень тонкую трубку и опустите один ее конец в чернила (фиг. 122, а ). Окрашенная вода поднимается вверх вопреки силе тяжести, опровергая правило: «вода в сообщающихся сосудах устанавливается на одном уровне». Однако в U-образной трубке с колонами разного сечения жидкость все же устанавливается на одном уровне (фиг. 122, б ). Если вспомнить обсуждение относительной роли поверхностных и объемных эффектов, можно догадаться, что влияние поверхностного натяжения будет более заметно в приборах малых размеров; например, в небольшой U-образной трубке (фиг. 122, в ). Конечно, это то же самое, что мы уже видели при погружении тонкой трубки в чернила.

Наброски, представленные на фиг. 122, г , помогают понять переход от одного опыта к другому. Если жидкость поднимается в тонких трубках, то в еще более тонких она должна подняться еще выше. Проверьте это (см. фиг. 122, д ).

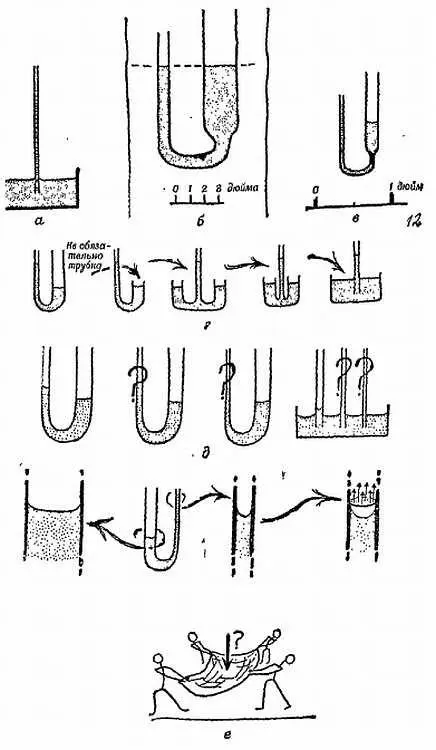
Фиг. 122. Капиллярные явления.

Поскольку это следствие поверхностного натяжения проявляется в трубках, «тонких, как волос», оно получило название от латинского слова «волос» — capilla . Таким образом, капиллярность — это старое название поверхностного натяжения, которое еще применяется, чтобы охарактеризовать поведение жидкостей в тонких трубках. Это красивое название, но оно не объясняет подъема жидкости. Сказать, что вода поднимается по тонкой трубке вследствие капиллярности, по существу то же, что сказать «вследствие поведения тонких трубок». Рассматривая через увеличительное стекло мениск (поверхность жидкости) в тонкой трубке, мы увидим, что он висит, как прикрепленный к стеклу изогнутый мешок, весьма похожий на одеяло пожарников, которые ловят выбрасывающегося из окна горящего дома тяжелого мужчину (фиг. 122, е ).

Снова возникает мысль о резиновой оболочке. Если измерить силы, удерживающие оболочку, то видно, что эти же силы определяют форму маленьких капель. Можно даже говорить, что оболочка удерживает поднимающуюся по трубке жидкость [75] Эта идея может позволить вывести формулу для измерения поверхностного натяжения Т , действующего на каждый сантиметр границы поверхности жидкости: ( тянущая сила со стороны оболочки ) = ( вес жидкости, удерживаемой в трубке ); Т ∙(Длина границы 2π r ) = [Объем (π r 2 )∙(Высота подъема)]∙(Плотность жидкости)∙(Ускорение силы тяжести g ) (эту формулу раньше очень любили составителя экзаменационных вопросов). Таким образом, Т = 1 / 2 g ∙(Плотность)∙(Высота подъема)∙(Радиус трубки). Эта формула более или менее верна, и ее используют для грубых определений Т , но сам вывод граничит с надувательством. На самом деле нет никакой резиновой оболочки, прикрепленной к стеклу, и в реальной формуле Т относится к поверхности раздела жидкость/воздух, а не является силой сцепления со стеклом. Но искривленная поверхность (мениск) реально существует, и, как в любом воздушном шаре, давление «внутри» (над мениском) больше, чем снаружи. С помощью этой разности давлений можно объяснить подъем жидкости в капилляре и дать строгий вывод формулы. , но более реально говорить о молекулах, которые вскарабкиваются по внутренней поверхности трубки и образуют изогнутый мениск.