Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Фиг. 137. Единичное ( а) и удвоенное ( б) ускорение.

Чтобы приложить к исследуемому телу всевозможные силы величиной 1, 2, 3, 4… странга, возьмем несколько одинаковых пружин [86] Вопрос о том, что значит сделать силы «равными» и сложить их, рассмотрев дальше в этой главе. . Затем сообщим телу ускорение силой 1 странг, 2, 3…, ускорения должны находиться в пропорции 1:2:3., значит для данного тела ускорение возрастает в такой же пропорции, что и ускоряющая сила, т. е. a ~ F .

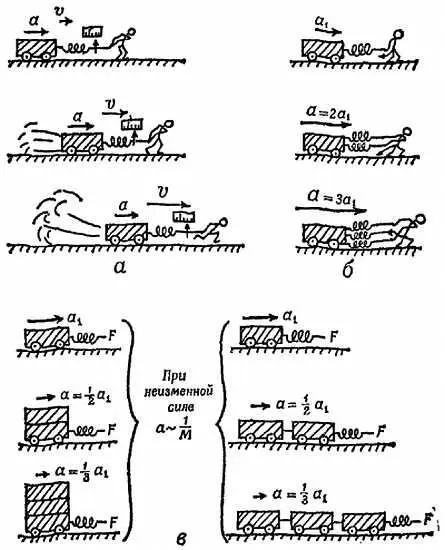
Фиг. 138. Удвоенные и утроенные массы.

а— постоянная сила сообщает телу постоянное ускорение; б— при неизменной массе ускорение пропорционально силе; в— при неизменной силе ускорение пропорционально 1/ М .

До сих пор мы всегда прикладывали силу к одному и тому же телу. Перейдем теперь к другим телам, другим количествам движущегося вещества, к удвоенной и утроенной массе. Возьмем несколько идентичных тел (тележек или кусков льда). Чтобы получить удвоенную массу, свяжите две тележки (или поставьте одну на другую) и приложите силу 1 странг. Затем соедините три одинаковых тела и приложите к ним эту силу. При удвоенной массе мы должны получить половину ускорения, при утроенной — одну треть ускорения. Ускорение убывает в такой же пропорции, в какой возрастает масса, т. е, а ~ 1/ М , где М измерено путем подсчета числа тележек. Это соотношение труднее себе представить, поэтому зададим вопрос по-иному: как следует изменить силу, чтобы сообщить разным массам одинаковое ускорение! Телу с удвоенной массой 1 странг сообщает половину ускорения, поэтому первоначальное ускорение этому телу должны сообщить 2 странга. В таком случае, чтобы сообщить одинаковое ускорение единичной массе, удвоенной массе и утроенной массе, к ним нужно приложить силы, которые находятся в пропорции 1:2:3. Силы, которые нужно приложить, пропорциональны массам F ~ M . Здесь, говоря о массе, мы имеем в виду количество вещества, которому нужно придать ускорение, количество одинаковых тележек (или кусков льда).

Резюме

Итак, мы получили два важных соотношения:

1) При неизменной массе

(Ускорение) ~ (Сила) , или (Сила) ~ (Ускорение).

2) При неизменном ускорении (Сила) ~ (Масса).

Эти соотношения можно объединить в одно [87] Алгебраическая сторона такого объединения пояснена в подстрочном примечании на стр. 253. Здесь можно сравнить это соотношение с выражением для подсчета стоимости рабочей силы при выполнении той или иной работы: (Стоимость) ~ (Число работающих) , (Стоимость) ~ (Число часов работы) . Объединение этих двух формул дает: (Стоимость) ~ (Число работающих)∙(Число часов) .

СИЛА ~ МАССА∙УСКОРЕНИЕ

или

СИЛА = (ПОСТОЯННАЯ)∙МАССА∙УСКОРЕНИЕ.

Второй закон движения Ньютона

Снова представим себе, что мы можем прикладывать постоянные силы к движущимся массам и точно измерять ускорения. Кроме того, предположим, что сила наших пружин — это единственная действующая на тело горизонтальная сила, которая, таким образом, является результирующей силой. Приведенное нами соотношение

РЕЗУЛЬТИРУЮЩАЯ СИЛА ~ МАССА∙УСКОРЕНИЕ

действительно справедливо. Это великий второй закон движения Ньютона (который включает первый закон Ньютона и предполагает выполнение его третьего закона при любой экспериментальной проверке).

Этот закон, связывающий силу, ускорение и массу, чрезвычайно важен для последующих разделов физики. Он подтверждается экспериментально для движения всех больших тел, от детских автомобилей и теннисных мячей до реактивных самолетов и планет; мы распространим его, кроме того, на атомы, электроны и ядра.

Чтобы понять этот закон и научиться им пользоваться, нужно уяснить его экспериментальную основу и исходные определения.

Поэтому очень важно посмотреть опыты. Прежде чем описать некоторые демонстрационные опыты, рассмотрим частный случай F = 0.

Нет сил — движение неизменно: первый закон Ньютона

Если F~ M∙ a, то в частном случае F = 0 ускорение должна быть равно нулю, т. е. движение должно продолжаться без изменений. К этому выводу можно прийти, анализируя движение снаряда: вертикальное ускорение есть результат действия земного притяжения, в горизонтальном движении также следует усматривать результат действия некой горизонтальной силы. Помимо сопротивления воздуха (которое в идеальном случае не участвует), никаких горизонтальных сил нет. Тем не менее пушечное ядро продолжает двигаться вперед с постоянной горизонтальной скоростью.