В 1955 г. было дано вполне разумное объяснение указанному парадоксу. Звезда высокой светимости в паре обладала большей массой вначале . Однако, исчерпав существенную часть своего ядерного горючего, она стала «раздуваться». При этом довольно значительная часть ее массы «перетекла» на соседнюю компоненту, отчего масса последней стала превышать массу более быстро эволюционирующей звезды. Таким образом, важнейшим процессом, определяющим эволюцию звезд в двойной системе, является обмен массами между ними. Поэтому нельзя рассматривать эволюцию звезд в двойных системах как проходящую с постоянной массой.
Как же происходит процесс обмена материей между компонентами двойной системы? Рассмотрим двойную систему, массы компонент которой M 1и M 2, а орбита круговая радиуса a . Тогда из простой теории тяготения следует, что существуют для каждой из компонент такие поверхности, за пределами которых частицы вещества уже не сдерживаются гравитационным притяжением соответствующей звезды. Это объясняется действием на указанные частицы гравитационного притяжения от второй звезды, а также центробежной силы, обусловленной общим вращением системы. Если частицы находятся на самих этих поверхностях, достаточно им сообщить сколь угодно малую скорость, направленную «наружу», и они уйдут из сферы притяжения этой звезды. Если же частицы находятся в области, окружающей точку L 1(рис. 14.1), то они, покидая первую звезду, будут захвачены притяжением ее соседки. Поверхность, обладающая такими свойствами, называется «поверхностью нулевой скорости», или «критической поверхностью Роша», а точка L 1, через которую вещество может перетекать из одной звезды в другую,— «внутренней лагранжевой точкой».
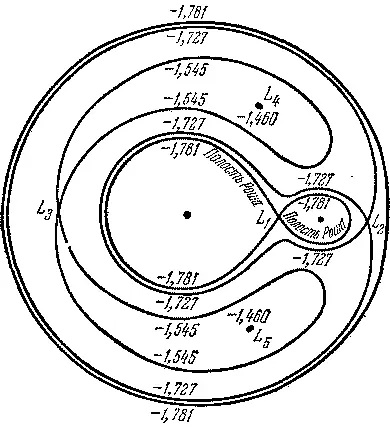 |
| Рис. 14.1:Схема поверхности Роша. |
|
Поверхность Роша состоит из двух замкнутых полостей, окружающих обе звезды и имеющих общую точку L 1. Радиус каждой из таких полостей может быть представлен приближенной формулой
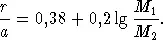 |
(14.1) |
Формула (14.1) дает вполне удовлетворительную точность для 0 , 3 < M 1 /M 2 < 20.
Рассмотрим теперь следующую модель эволюции звезд в тесной двойной системе. Пока обе компоненты двойной системы пребывали на главной последовательности, их радиусы были меньше радиусов соответствующих полостей Роша, определяемых формулой (14.1). Когда исчерпается значительная часть водородного горючего в центральной части быстрее эволюционирующей более массивной звезды, радиус последней станет увеличиваться , в то время как радиус второй компоненты останется неизменным. Таким образом, более массивная компонента станет «разбухать», пока ее наружная часть не заполнит свою полость Роша (см. рис. 14.1). После этого расширение главной компоненты прекратится, так как избыточная ее масса, выходящая за пределы полости Роша, начнет «переливаться» во вторую компоненту, масса которой начнет расти .
Скорость потери массы эволюционирующей звездой очень быстро растет по мере роста радиуса этой звезды после достижения им величины радиуса полости Роша. Расчеты показывают, что убыль массы за единицу времени q дается формулой
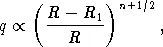 |
(14.2) |
где величина n зависит от структуры звезды (так называемый «политропный индекс»). Можно принять, что n = 3, и тогда для того, чтобы обмен массами между компонентами двойной системы шел в более или менее приемлемом темпе, необходимо, чтобы 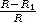 было меньше 0,03. Это означает, что на стадии эволюции, когда масса перетекает от одной компоненты ко второй, радиус эволюционирующей звезды должен все время оставаться очень близким к радиусу полости Роша.
было меньше 0,03. Это означает, что на стадии эволюции, когда масса перетекает от одной компоненты ко второй, радиус эволюционирующей звезды должен все время оставаться очень близким к радиусу полости Роша.
В первом приближении можно принять, что в процессе эволюции газ, выброшенный эволюционирующей звездой, не покинет пределы двойной системы, т. е. ее полная масса M = M 1+ M 2сохраняется. При таком вполне естественном предположении расстояние между компонентами будет в процессе эволюции меняться согласно формуле
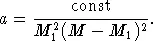 |
(14.3) |
Можно убедиться, что минимальное расстояние между компонентами двойной системы будет тогда, когда в процессе «перекачки» массы от эволюционирующей компоненты к неэволюционирующей массы обеих звезд сравняются.
Читать дальше


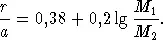
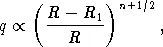
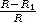 было меньше 0,03. Это означает, что на стадии эволюции, когда масса перетекает от одной компоненты ко второй, радиус эволюционирующей звезды должен все время оставаться очень близким к радиусу полости Роша.
было меньше 0,03. Это означает, что на стадии эволюции, когда масса перетекает от одной компоненты ко второй, радиус эволюционирующей звезды должен все время оставаться очень близким к радиусу полости Роша.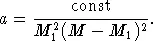





![Андрэ Нортон - Рожденные среди звезд [= Рождение звезды]](/books/322400/andre-norton-rozhdennye-sredi-zvezd-rozhdenie-zve-thumb.webp)
![Эдвард Радзинский - Тираны России и СССР [Распутин. Жизнь и смерть + Сталин. Жизнь и смерть]](/books/391099/edvard-radzinskij-tirany-rossii-i-sssr-rasputin-thumb.webp)


