В центральной части «нормальной» звезды вес вещества, заключенного в столбе, площадь основания которого равна одному квадратному сантиметру, а высота — радиусу звезды, будет равен давлению газа у основания столба. С другой стороны, масса столба равна силе, с которой он притягивается к центру звезды.
Мы сейчас проведем весьма упрощенный расчет, который, тем не менее, вполне отражает существо вопроса. А именно, положим массу нашего столба M 1=  R , где
R , где  — средняя плотность звезды, и будем считать, что «эффективное» расстояние между центром звезды и основанием столба равно R/ 2. Тогда условие гидростатического равновесия запишется так:
— средняя плотность звезды, и будем считать, что «эффективное» расстояние между центром звезды и основанием столба равно R/ 2. Тогда условие гидростатического равновесия запишется так:
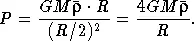 |
(6.1) |
Сделаем теперь оценку величины газового давления P в центральной части такой звезды, какой является наше Солнце. Подставив численное значение величин, стоящих в правой части этого уравнения, найдем, что P = 10 16дин/см 2, или 10 миллиардов атмосфер! Это неслыханно большая величина. Самое высокое «стационарное» давление, достигаемое в земных лабораториях, порядка нескольких миллионов атмосфер [ 17 ] Заметим, однако, что при фокусировке мощного лазерного луча на мишень (которая, конечно, при этом мгновенно испарится) в течение 10 - 9 секунды может возникнуть давление отдачи на нее (обусловленное испаряющимися атомами), достигающее 10 12 атмосфер!
.
Из элементарного курса физики известно, что давление газа зависит от его плотности 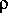 и температуры T . Формула, связывающая все эти величины, носит название «формулы Клапейрона»: P =
и температуры T . Формула, связывающая все эти величины, носит название «формулы Клапейрона»: P = 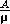
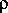 T . С другой стороны, плотность в центральных областях «нормальных» звезд, конечно, больше, чем средняя плотность, но не существенно больше. В таком случае, из формулы Клапейрона непосредственно следует, что одна лишь большая плотность звездных недр сама по себе не в состоянии обеспечить достаточно высокое давление газа, чтобы выполнялось условие гидростатического равновесия. Необходимо прежде всего, чтобы температура газа была достаточно высока.
T . С другой стороны, плотность в центральных областях «нормальных» звезд, конечно, больше, чем средняя плотность, но не существенно больше. В таком случае, из формулы Клапейрона непосредственно следует, что одна лишь большая плотность звездных недр сама по себе не в состоянии обеспечить достаточно высокое давление газа, чтобы выполнялось условие гидростатического равновесия. Необходимо прежде всего, чтобы температура газа была достаточно высока.
В формулу Клапейрона входит также средняя молекулярная масса 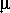 . Основным химическим элементом в атмосферах звезд является водород, и нет оснований полагать, что в недрах по крайней мере большинства звезд химический состав должен существенно отличаться от наблюдаемого в наружных слоях. В то же время, так как ожидаемая температура в центральных областях звезд должна быть достаточно велика, водород там должен быть почти полностью ионизован, т. е. «расщеплен» на протоны и электроны. Так как масса последних пренебрежимо мала по сравнению с протонами, а количество протонов равно количеству электронов, то средняя молекулярная масса этой смеси должна быть близка к 1 / 2. Тогда из уравнений (6.1) и формулы Клапейрона следует, что температура в центральных областях звезд по порядку величин равна
. Основным химическим элементом в атмосферах звезд является водород, и нет оснований полагать, что в недрах по крайней мере большинства звезд химический состав должен существенно отличаться от наблюдаемого в наружных слоях. В то же время, так как ожидаемая температура в центральных областях звезд должна быть достаточно велика, водород там должен быть почти полностью ионизован, т. е. «расщеплен» на протоны и электроны. Так как масса последних пренебрежимо мала по сравнению с протонами, а количество протонов равно количеству электронов, то средняя молекулярная масса этой смеси должна быть близка к 1 / 2. Тогда из уравнений (6.1) и формулы Клапейрона следует, что температура в центральных областях звезд по порядку величин равна
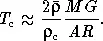 |
(6.2) |
Величина  /
/ 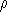 c может быть порядка 1 / 10. Она зависит от структуры звездных недр (см. § 12). Из формулы (6.2) следует, что температура в центральных областях Солнца должна быть порядка десяти миллионов кельвинов. Более точные расчеты отличаются от полученной нами сейчас оценки всего лишь на 20—30%. Итак, температура в центральных областях звезд исключительно велика — примерно в тысячу раз больше, чем на их поверхности. Теперь обсудим, каковы должны быть свойства вещества, нагретого до такой высокой температуры. Прежде всего такое вещество, несмотря на свою большую плотность, должно находиться в газообразном состоянии. Об этом речь уже шла выше. Но мы можем теперь уточнить это утверждение. При такой высокой температуре свойства газа в недрах звезд, несмотря на его высокую плотность, будут почти неотличимы от свойств идеального газа , т. е. такого газа, в котором взаимодействия между составляющими его частицами (атомами, электронами, ионами) сводятся к столкновениям. Именно для идеального газа справедлив закон Клапейрона, которым мы воспользовались при оценке температуры в центральных областях звезд.
c может быть порядка 1 / 10. Она зависит от структуры звездных недр (см. § 12). Из формулы (6.2) следует, что температура в центральных областях Солнца должна быть порядка десяти миллионов кельвинов. Более точные расчеты отличаются от полученной нами сейчас оценки всего лишь на 20—30%. Итак, температура в центральных областях звезд исключительно велика — примерно в тысячу раз больше, чем на их поверхности. Теперь обсудим, каковы должны быть свойства вещества, нагретого до такой высокой температуры. Прежде всего такое вещество, несмотря на свою большую плотность, должно находиться в газообразном состоянии. Об этом речь уже шла выше. Но мы можем теперь уточнить это утверждение. При такой высокой температуре свойства газа в недрах звезд, несмотря на его высокую плотность, будут почти неотличимы от свойств идеального газа , т. е. такого газа, в котором взаимодействия между составляющими его частицами (атомами, электронами, ионами) сводятся к столкновениям. Именно для идеального газа справедлив закон Клапейрона, которым мы воспользовались при оценке температуры в центральных областях звезд.
Читать дальше

 R , где
R , где  — средняя плотность звезды, и будем считать, что «эффективное» расстояние между центром звезды и основанием столба равно R/ 2. Тогда условие гидростатического равновесия запишется так:
— средняя плотность звезды, и будем считать, что «эффективное» расстояние между центром звезды и основанием столба равно R/ 2. Тогда условие гидростатического равновесия запишется так: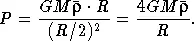
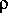 и температуры T . Формула, связывающая все эти величины, носит название «формулы Клапейрона»: P =
и температуры T . Формула, связывающая все эти величины, носит название «формулы Клапейрона»: P = 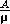
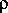 T . С другой стороны, плотность в центральных областях «нормальных» звезд, конечно, больше, чем средняя плотность, но не существенно больше. В таком случае, из формулы Клапейрона непосредственно следует, что одна лишь большая плотность звездных недр сама по себе не в состоянии обеспечить достаточно высокое давление газа, чтобы выполнялось условие гидростатического равновесия. Необходимо прежде всего, чтобы температура газа была достаточно высока.
T . С другой стороны, плотность в центральных областях «нормальных» звезд, конечно, больше, чем средняя плотность, но не существенно больше. В таком случае, из формулы Клапейрона непосредственно следует, что одна лишь большая плотность звездных недр сама по себе не в состоянии обеспечить достаточно высокое давление газа, чтобы выполнялось условие гидростатического равновесия. Необходимо прежде всего, чтобы температура газа была достаточно высока.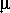 . Основным химическим элементом в атмосферах звезд является водород, и нет оснований полагать, что в недрах по крайней мере большинства звезд химический состав должен существенно отличаться от наблюдаемого в наружных слоях. В то же время, так как ожидаемая температура в центральных областях звезд должна быть достаточно велика, водород там должен быть почти полностью ионизован, т. е. «расщеплен» на протоны и электроны. Так как масса последних пренебрежимо мала по сравнению с протонами, а количество протонов равно количеству электронов, то средняя молекулярная масса этой смеси должна быть близка к 1 / 2. Тогда из уравнений (6.1) и формулы Клапейрона следует, что температура в центральных областях звезд по порядку величин равна
. Основным химическим элементом в атмосферах звезд является водород, и нет оснований полагать, что в недрах по крайней мере большинства звезд химический состав должен существенно отличаться от наблюдаемого в наружных слоях. В то же время, так как ожидаемая температура в центральных областях звезд должна быть достаточно велика, водород там должен быть почти полностью ионизован, т. е. «расщеплен» на протоны и электроны. Так как масса последних пренебрежимо мала по сравнению с протонами, а количество протонов равно количеству электронов, то средняя молекулярная масса этой смеси должна быть близка к 1 / 2. Тогда из уравнений (6.1) и формулы Клапейрона следует, что температура в центральных областях звезд по порядку величин равна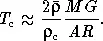
 /
/ 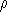 c может быть порядка 1 / 10. Она зависит от структуры звездных недр (см. § 12). Из формулы (6.2) следует, что температура в центральных областях Солнца должна быть порядка десяти миллионов кельвинов. Более точные расчеты отличаются от полученной нами сейчас оценки всего лишь на 20—30%. Итак, температура в центральных областях звезд исключительно велика — примерно в тысячу раз больше, чем на их поверхности. Теперь обсудим, каковы должны быть свойства вещества, нагретого до такой высокой температуры. Прежде всего такое вещество, несмотря на свою большую плотность, должно находиться в газообразном состоянии. Об этом речь уже шла выше. Но мы можем теперь уточнить это утверждение. При такой высокой температуре свойства газа в недрах звезд, несмотря на его высокую плотность, будут почти неотличимы от свойств идеального газа , т. е. такого газа, в котором взаимодействия между составляющими его частицами (атомами, электронами, ионами) сводятся к столкновениям. Именно для идеального газа справедлив закон Клапейрона, которым мы воспользовались при оценке температуры в центральных областях звезд.
c может быть порядка 1 / 10. Она зависит от структуры звездных недр (см. § 12). Из формулы (6.2) следует, что температура в центральных областях Солнца должна быть порядка десяти миллионов кельвинов. Более точные расчеты отличаются от полученной нами сейчас оценки всего лишь на 20—30%. Итак, температура в центральных областях звезд исключительно велика — примерно в тысячу раз больше, чем на их поверхности. Теперь обсудим, каковы должны быть свойства вещества, нагретого до такой высокой температуры. Прежде всего такое вещество, несмотря на свою большую плотность, должно находиться в газообразном состоянии. Об этом речь уже шла выше. Но мы можем теперь уточнить это утверждение. При такой высокой температуре свойства газа в недрах звезд, несмотря на его высокую плотность, будут почти неотличимы от свойств идеального газа , т. е. такого газа, в котором взаимодействия между составляющими его частицами (атомами, электронами, ионами) сводятся к столкновениям. Именно для идеального газа справедлив закон Клапейрона, которым мы воспользовались при оценке температуры в центральных областях звезд.




![Андрэ Нортон - Рожденные среди звезд [= Рождение звезды]](/books/322400/andre-norton-rozhdennye-sredi-zvezd-rozhdenie-zve-thumb.webp)
![Эдвард Радзинский - Тираны России и СССР [Распутин. Жизнь и смерть + Сталин. Жизнь и смерть]](/books/391099/edvard-radzinskij-tirany-rossii-i-sssr-rasputin-thumb.webp)


